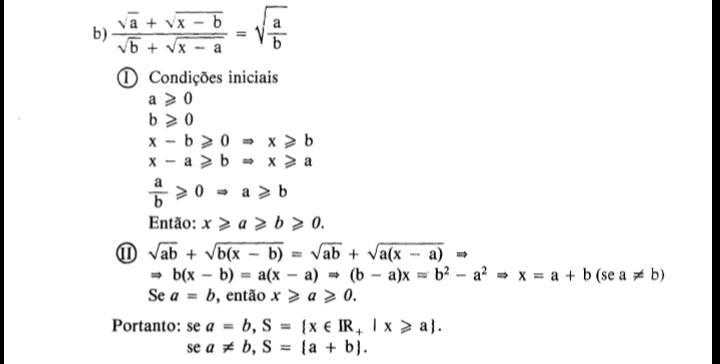Equação irracional
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Luís Yanky- Iniciante
- Mensagens : 35
Data de inscrição : 08/11/2020
Idade : 21
Localização : Fortaleza-CE
 Re: Equação irracional
Re: Equação irracional
[latex] \frac{\sqrt{a} + \sqrt{x - b}}{\sqrt{b} + \sqrt{x - a}} = \frac{\sqrt{a}}{\sqrt{b}} \rightarrow \sqrt{ab} + \sqrt{b(x-b)} = \sqrt{ab} + \sqrt{a(x-a)} \\ \\ \rightarrow \sqrt{b(x-b)} = \sqrt{a(x-a)} \rightarrow b(x - b) = a(x-a) \rightarrow x(b - a) = b^2 - a^2 \\
1^o \: Caso: a \neq b \rightarrow x(b-a) = (b - a)(b + a) \rightarrow S = \left \{ x \: \epsilon \: \mathbb{R} \: / x = a+b \right \} \: \\
2^o \: Caso: a = b\rightarrow x.0 = 0.(b+a) \rightarrow S = \left \{ x \: \epsilon \: \mathbb{R} \: / \: x \geq a \right \} \: [/latex]
No segundo caso, x deve ser >= a para satisfazer a condição de existência da raiz.
Creio que seja isso.
1^o \: Caso: a \neq b \rightarrow x(b-a) = (b - a)(b + a) \rightarrow S = \left \{ x \: \epsilon \: \mathbb{R} \: / x = a+b \right \} \: \\
2^o \: Caso: a = b\rightarrow x.0 = 0.(b+a) \rightarrow S = \left \{ x \: \epsilon \: \mathbb{R} \: / \: x \geq a \right \} \: [/latex]
No segundo caso, x deve ser >= a para satisfazer a condição de existência da raiz.
Creio que seja isso.

Leonardo Mariano- Monitor

- Mensagens : 647
Data de inscrição : 11/11/2018
Idade : 22
Localização : Criciúma/SC
 Re: Equação irracional
Re: Equação irracional
Obrigado pela solução. Eu estava olhando a resolução que o livro traz, e o autor diz o seguinte:
a/b ≥ 0 (até aqui ok)
a ≥ b (??)
Saberia explicar?
a/b ≥ 0 (até aqui ok)
a ≥ b (??)
Saberia explicar?
Luís Yanky- Iniciante
- Mensagens : 35
Data de inscrição : 08/11/2020
Idade : 21
Localização : Fortaleza-CE
 Re: Equação irracional
Re: Equação irracional
Poste a solução completa do seu livro, pra ser analisada.

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Luís Yanky- Iniciante
- Mensagens : 35
Data de inscrição : 08/11/2020
Idade : 21
Localização : Fortaleza-CE
 Re: Equação irracional
Re: Equação irracional
Existe dois erros em I:
a ≥ 0
b ≥ 0
x - b ≥ 0 ---> x ≥ b
x - a ≥ 0 ---> x ≥ a
a/b ≥ 0 ---> Existem três possibilidades;
1) Se a/b = 0 ---> a = 0 e b ≠ 0 ---> a < b
2) Se a/b = 0,5 (por exemplo) ---> a < b
3) Se a/b = 2 (por exemplo) ---> a > b
Para mim esta solução do livro não está correta. Não olhei o restante dela.
a ≥ 0
b ≥ 0
x - b ≥ 0 ---> x ≥ b
x - a ≥ 0 ---> x ≥ a
a/b ≥ 0 ---> Existem três possibilidades;
1) Se a/b = 0 ---> a = 0 e b ≠ 0 ---> a < b
2) Se a/b = 0,5 (por exemplo) ---> a < b
3) Se a/b = 2 (por exemplo) ---> a > b
Para mim esta solução do livro não está correta. Não olhei o restante dela.

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Equação irracional
Re: Equação irracional
Obrigado!
Luís Yanky- Iniciante
- Mensagens : 35
Data de inscrição : 08/11/2020
Idade : 21
Localização : Fortaleza-CE
 Tópicos semelhantes
Tópicos semelhantes» Equação Irracional
» Equação irracional.
» Equação irracional 4
» equação irracional
» Equação Irracional
» Equação irracional.
» Equação irracional 4
» equação irracional
» Equação Irracional
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos