Medida PQ
4 participantes
Página 1 de 1

melissa_miranda- Recebeu o sabre de luz

- Mensagens : 118
Data de inscrição : 15/01/2019
Idade : 24
Localização : Pirapora - Minas Gerais, Brasil

raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro

jessesantos2001- Padawan

- Mensagens : 71
Data de inscrição : 20/02/2018
Idade : 23
Localização : mage rio de janeiro
melissa_miranda gosta desta mensagem
 Re: Medida PQ
Re: Medida PQ
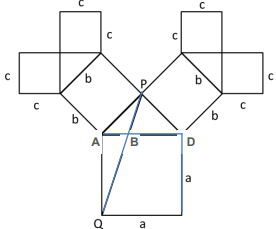
Acredito ter feito de uma terceira forma:
Através dos quadrados de lados c se percebe o triângulo retângulo de catetos c e hipotenusa b:
b² = c² + c² -> b = c√2 (I)
O triângulo PAD é retângulo, possuindo catetos b e hipotenusa a:
a² = b² + b²
De (I):
(c√2)² + (c√2)² = 2c² + 2c² = 4c² -> a = 2c (II)
Traçando o ponto E, médio entre AD, se tem um triângulo retângulo AEP, tal que seus catetos são a/2 e x e hipotenusa b:
b² = (a/2)² + x²
De (I) e (II):
(c√2)² = (2c/2)² + x² -> 2c² = c² + x² -> x² = 2c² - c² = c² -> x = c (III)
Chamando o vértice inferior direito do quadrado de lado a de F, traça-se o ponto G, médio entre QF, formando um triângulo retângulo QGP, tal que seus catetos são a/2, a + x e sua hipotenusa QP:
QP² = (a/2)² + (a + x)²
De (I), (II) e (III):
QP² = (2c/2)² + (2c + c)² = c² + 9c² = 10c² -> QP = c√10
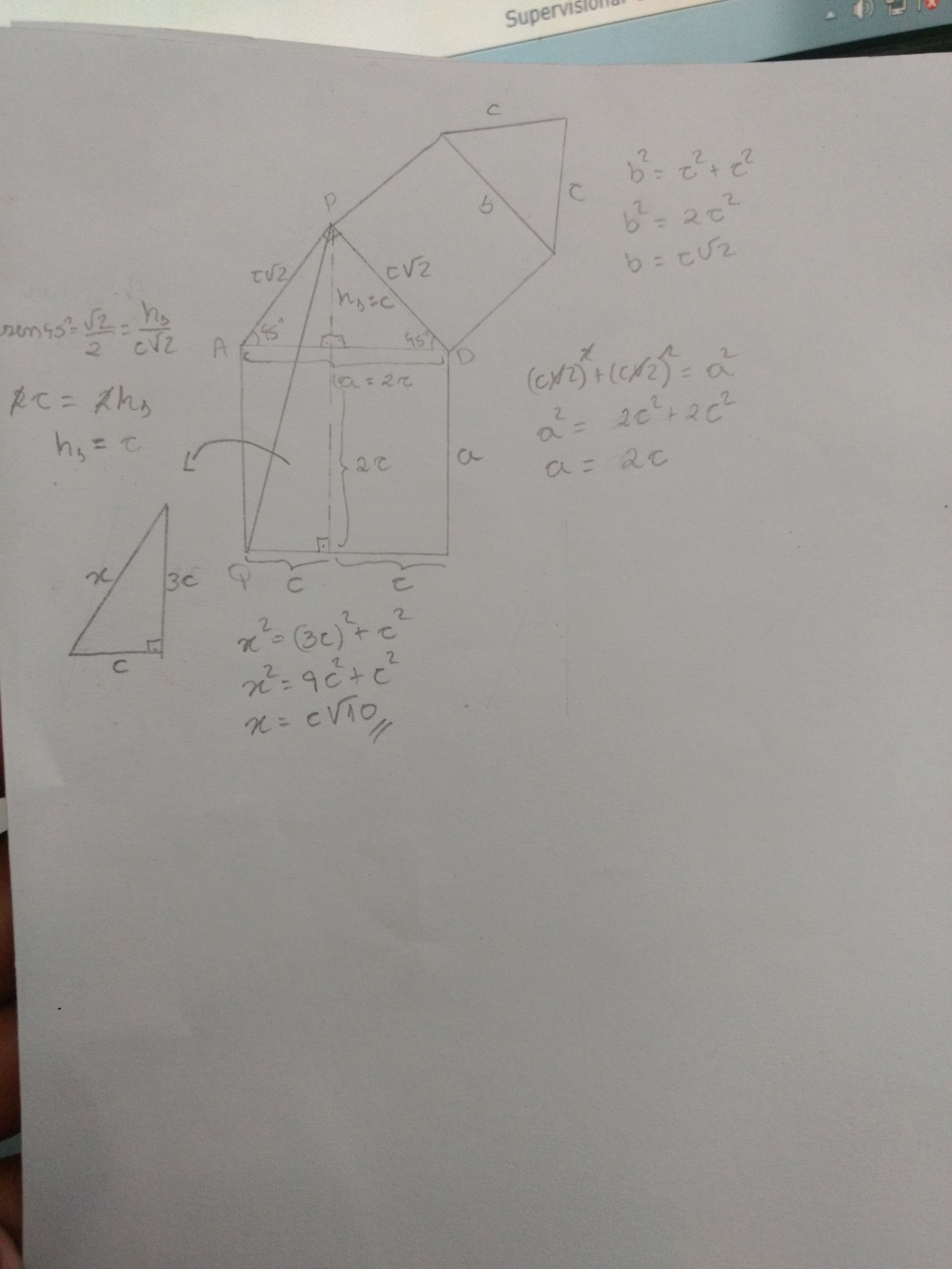
Através dos quadrados de lados c se percebe o triângulo retângulo de catetos c e hipotenusa b:
b² = c² + c² -> b = c√2 (I)
O triângulo PAD é retângulo, possuindo catetos b e hipotenusa a:
a² = b² + b²
De (I):
(c√2)² + (c√2)² = 2c² + 2c² = 4c² -> a = 2c (II)
Traçando o ponto E, médio entre AD, se tem um triângulo retângulo AEP, tal que seus catetos são a/2 e x e hipotenusa b:
b² = (a/2)² + x²
De (I) e (II):
(c√2)² = (2c/2)² + x² -> 2c² = c² + x² -> x² = 2c² - c² = c² -> x = c (III)
Chamando o vértice inferior direito do quadrado de lado a de F, traça-se o ponto G, médio entre QF, formando um triângulo retângulo QGP, tal que seus catetos são a/2, a + x e sua hipotenusa QP:
QP² = (a/2)² + (a + x)²
De (I), (II) e (III):
QP² = (2c/2)² + (2c + c)² = c² + 9c² = 10c² -> QP = c√10
melissa_miranda gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos