Perimetro triangulo - Colegio naval
3 participantes
Página 1 de 1
Perimetro triangulo - Colegio naval
por felipe00_1 Sex 29 maio 2020, 17:20
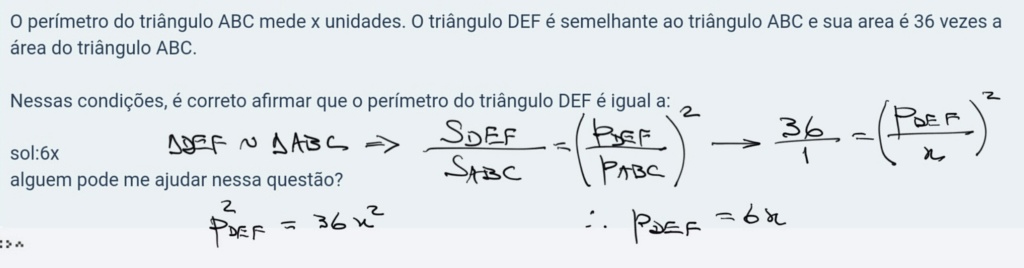
O perímetro do triângulo ABC mede x unidades. O triângulo DEF é semelhante ao triângulo ABC e sua area é 36 vezes a área do triângulo ABC.
Nessas condições, é correto afirmar que o perímetro do triângulo DEF é igual a:
sol:6x
alguem pode me ajudar nessa questão?
Nessas condições, é correto afirmar que o perímetro do triângulo DEF é igual a:
sol:6x
alguem pode me ajudar nessa questão?
felipe00_1- Recebeu o sabre de luz
- Mensagens : 134
Data de inscrição : 13/07/2017
Idade : 26
Localização : Canoas, Rio grande do sul
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10409
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Perimetro triangulo - Colegio naval
por Elcioschin Sex 29 maio 2020, 17:54
Outro modo, mais detalhado, usando Heron:
semiperímetro = x/2 = (a + b + c)/2
S = √(x/2).(x/2 - a).(x/2 - b).(x/2 - c)
S² = (x/2).(x/2 - a).(x/2 - b).(x/2 - c)
Novo triângulo: lados k.a, k.b, k.c ---> x'/2 = k.x/2
S'² = (k.x/2).(k.x/2 - k.a).(k.x/2 - k.b).(k.x/2 - k.c) --->
S'² = k4.(x/2).(x/2 - a).(x/2 - b).(x/2 - c)
S'² = k4.S²
S' = k².S ---> S' = 36.S ---> k² = 36 ---> k = 6
x' = k.x ---> x' = 6.x
semiperímetro = x/2 = (a + b + c)/2
S = √(x/2).(x/2 - a).(x/2 - b).(x/2 - c)
S² = (x/2).(x/2 - a).(x/2 - b).(x/2 - c)
Novo triângulo: lados k.a, k.b, k.c ---> x'/2 = k.x/2
S'² = (k.x/2).(k.x/2 - k.a).(k.x/2 - k.b).(k.x/2 - k.c) --->
S'² = k4.(x/2).(x/2 - a).(x/2 - b).(x/2 - c)
S'² = k4.S²
S' = k².S ---> S' = 36.S ---> k² = 36 ---> k = 6
x' = k.x ---> x' = 6.x
Elcioschin- Grande Mestre
- Mensagens : 71863
Data de inscrição : 15/09/2009
Idade : 77
Localização : Santos/SP
Re: Perimetro triangulo - Colegio naval
por Medeiros Sex 29 maio 2020, 18:39
Outro modo, usando o conceito de semelhança de forma mais simples.
Seja k a razão de semelhança entre os triângulos DEF e ABC. Então todos os elementos lineares de um triângulo são k vezes os elementos homólogos do outro.
E seja b uma base do triângulo e h a altura referente a esta base.
_ABC_ ............. _DEF_
... b ..................... b' = k.b
... h ..................... h' = k.h
.. S = b.h/2 ......... S' = (kb).(kh)/2 = k2.b.h/2
.:. S' = k2.S -----> k2 = S'/S -----> k2 = 36 -----> k = 6
p = pABC = a + b + c = x
p' = pDEF = a' + b' + c' = k.a + k.b + k.c = k.(a + b + c)
.:. p' = k.p -----> p' = 6.x
Seja k a razão de semelhança entre os triângulos DEF e ABC. Então todos os elementos lineares de um triângulo são k vezes os elementos homólogos do outro.
E seja b uma base do triângulo e h a altura referente a esta base.
_ABC_ ............. _DEF_
... b ..................... b' = k.b
... h ..................... h' = k.h
.. S = b.h/2 ......... S' = (kb).(kh)/2 = k2.b.h/2
.:. S' = k2.S -----> k2 = S'/S -----> k2 = 36 -----> k = 6
p = pABC = a + b + c = x
p' = pDEF = a' + b' + c' = k.a + k.b + k.c = k.(a + b + c)
.:. p' = k.p -----> p' = 6.x
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10409
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» Perímetro do triângulo
» perímetro do triângulo
» Perímetro do triângulo
» Perímetro de um triângulo
» Perímetro do triângulo.
» perímetro do triângulo
» Perímetro do triângulo
» Perímetro de um triângulo
» Perímetro do triângulo.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
