Comprimento de linha passando pela interseção de círc.

por odeprimido Dom 26 maio 2019, 11:59

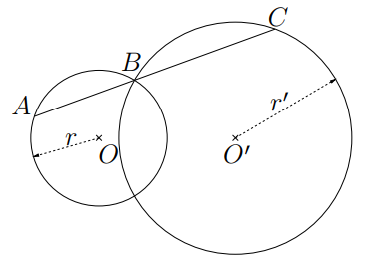
Na Figura, as cordas AB e BC estão alinhadas. Determine a característica que faça com que o comprimento de AC seja máximo.

(a) O ponto extremo A deve estar alinhado com OO'
(b) AB deve ser igual a BC
(c) AB/r = BC/r'
(d) AC deve ser paralelo a OO'

Gabarito: (d)

Comprimento de linha passando pela interseção de círc. Sem_tz10

Gostaria de ajuda com essa questão. Muito obrigado, desde já.

por **Elcioschin** Dom 26 maio 2019, 13:11

Trace OA = OB = r e O'B = O'C = r' e sejam M e N os pontos médios de AB e BC.
Trace OM e O'N ---> AÔM = BÔM = α/2 ---> BÔ'N = CÔ'N = β/2

Sejam AÔB = α e BO'C = β

AB = AM + BM ---> AB = r.sen(α/2) + r.sen(α/2) ---> AB = 2.r.sen(α/2)

BC = BN + CN ---> Similar ---> BC = 2.r'.sen(β/2)

AC = AB + BC ---> AC = 2.r.sen(α/2) + 2.r'.sen(β/2)

Basta derivar e encontrar a relação ente α, β que implicam o valor máximo de AC

por odeprimido Dom 26 maio 2019, 16:16

Muito obrigado, Professor. Mas, ainda não consegui chegar à resposta. Como eu consigo obter uma relação entre α e β, para poder derivar como uma função de uma variável? Obrigado mais uma vez.

por **Medeiros** Dom 26 maio 2019, 16:36

pelo desenho, no golpe de vista, parece que os círculos são ortogonais; se forem, alfa+beta=pi.

por odeprimido Dom 26 maio 2019, 18:23

Obrigado, Medeiros. Mas, como essa informação não foi dada no problema, não acredito ser (necessariamente) o caso. Será que não sai de outra forma? Obrigado!

por **Medeiros** Ter 28 maio 2019, 02:18

verdade, Deprimido, apenas comentei pensando que essa questão poderia estar, como exercício, numa seção de livro onde se aborda círculos ortogonais; neste caso estaria implícito.

Mas, você tem razão, se essa informação específica não foi dada então não podemos considerar assim. E também não deve ser necessária para resolução.