Cone e esfera - Comprimento da linha de interseção

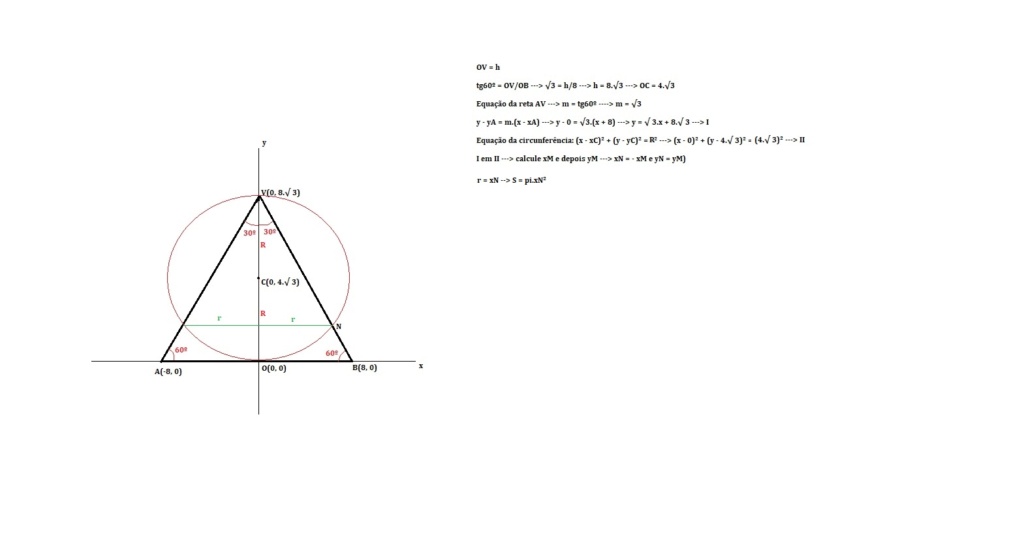
Uma superfície esférica tem como diâmetro a altura de um cone equilátero cujo raio da base é 8 cm. Calcule o comprimento da linha de interseção do cone com a superfície esférica.

Gabarito: \(12 \pi \)

Elcioschin escreveu:

Muito obrigado, mestre!

apenas com Geom. Plana




Na figura temos o corte meridiano do cone e da esfera de raio R cujo centro é O. Sendo o cone equilátero, o corte no plano meridiano é o triângulo equilátero ABC. Como a base do cone tem raio de medida 8, o triângulo tem lado 16, assim o diâmetro da esfera (2.R), que é a própria altura AM do triângulo, é dado por

A interseção da esfera e cone é uma circunferência de raio r cuja projeção neste plano de corte é o segmento DE.  Semelhante ao triâng. ABC, o triâng. ADE também é equilátero. Acontece que o triâng. ADE está inscrito na circunferência (círculo máx. da esfera), portanto o centro O é também baricentro de ADE, sendo AF altura e mediana. Como propriedade da mediana temos que

Por Pitágoras no triâng. retângulo OFE temos

(1) em (2), vem:

O comprimento L da circunferância da interseção é

Medeiros escreveu:apenas com Geom. Plana




Na figura temos o corte meridiano do cone e da esfera de raio R cujo centro é O. Sendo o cone equilátero, o corte no plano meridiano é o triângulo equilátero ABC. Como a base do cone tem raio de medida 8, o triângulo tem lado 16, assim o diâmetro da esfera (2.R), que é a própria altura AM do triângulo, é dado por

\( 2R=AM=16\frac{\sqrt{3}}{2}\ \rightarrow\ AM = 8\sqrt{3}\ \rightarrow\ \, R=4\sqrt{3}\,cm \)                (1)

A interseção da esfera e cone é uma circunferência de raio r cuja projeção neste plano de corte é o segmento DE.  Semelhante ao triâng. ABC, o triâng. ADE também é equilátero. Acontece que o triâng. ADE está inscrito na circunferência (círculo máx. da esfera), portanto o centro O é também baricentro de ADE, sendo AF altura e mediana. Como propriedade da mediana temos que

\( \frac{AO}{OF}=\frac{2}{1}\ \rightarrow \frac{R}{OF}=\frac{2}{1}\ \rightarrow\ \, OF=\frac{R}{2}\,cm \)

Por Pitágoras no triâng. retângulo OFE temos

\( r²=R²-(R/2)²\ \rightarrow\ r²=3R²/4\ \rightarrow\ \,r=R\frac{\sqrt{3}}{2} \)               (2)

(1) em (2), vem:

\( r=4\sqrt{3}.\frac{\sqrt{3}}{2}\ \rightarrow\ \boxed{\,r=6\,cm\,} \)

O comprimento L da circunferância da interseção é

\( L=2 \pi.r\ \rightarrow\ L=2. \pi.6\ \rightarrow\ \boxed{\,L=12\pi\,cm\,} \)

Excelente, Medeiros. Muito obrigado pela ajuda!

Medeiros escreveu:A interseção da esfera e cone é uma circunferência de raio r cuja projeção neste plano de corte é o segmento DE.  Semelhante ao triâng. ABC, o triâng. ADE também é equilátero. Acontece que o triâng. ADE está inscrito na circunferência (círculo máx. da esfera), portanto o centro O é também baricentro de ADE, sendo AF altura e mediana. Como propriedade da mediana temos que

\( \frac{AO}{OF}=\frac{2}{1}\ \rightarrow \frac{R}{OF}=\frac{2}{1}\ \rightarrow\ \, OF=\frac{R}{2}\,cm \)

Por Pitágoras no triâng. retângulo OFE temos

\( r²=R²-(R/2)²\ \rightarrow\ r²=3R²/4\ \rightarrow\ \,r=R\frac{\sqrt{3}}{2} \)               (2)

(1) em (2), vem:

\( r=4\sqrt{3}.\frac{\sqrt{3}}{2}\ \rightarrow\ \boxed{\,r=6\,cm\,} \)

Mestre, gostaria de colocar uma maneira alternativa de encontrarmos esse r, no intuito de complementar o tópico.
Podemos aproveitar as várias fórmulas para o cálculo da área de um triângulo. Como você disse, o triângulo menor também é equilátero, assim como ele está inscrito na circunferência desenhada. Temos, então:

\(S = \frac{l^2 \sqrt3}{4} = \frac{abc}{4R} \)

Sendo a primeira fórmula referente ao cálculo da área de um triângulo equilátero de lado l; e a segunda referente ao cálculo de um triângulo qualquer em função do raio de sua circunferência circunscrita, sendo a, b e c, os lados do triângulo, e R, o raio da circunferência. Portanto:

\(\frac{(2r)^2 \sqrt3}{4} = \frac{(2r)^3}{4R} \implies 2r = \sqrt3 \; . \; 4\sqrt3 \therefore \boxed{r=6cm}\)

Aí é só prosseguir com os cálculos.

Muito bom, Zeroberto! É até bem mais rápido do que eu fiz; se tivesse tido a ideia teria feito assim. Você enriqueceu o fórum.

Mas dá próxima vez dê uma indicação da conta que você vai fazer. Porque esta não era tão óbvia assim, e apesar de você mencionar várias fórmulas para calcular a área, levei um tempo até perceber que você igualou o cálculo da mesma área de duas formas diferentes.

Tem razão, Medeiros. Vou editar agora mesmo.

Ficou muito bom, Zeroberto.