Função e pontos críticos

por FalcolinoSheldon Sex 10 maio 2019, 22:46

Foi dada uma função f com lei de formação f(x) = - x^3 -x^2 -x -1 pediu-se para determinar se há uma reta tangente a x.
O domínio da função é: [-2 ,1] |----> B contido nos Reais

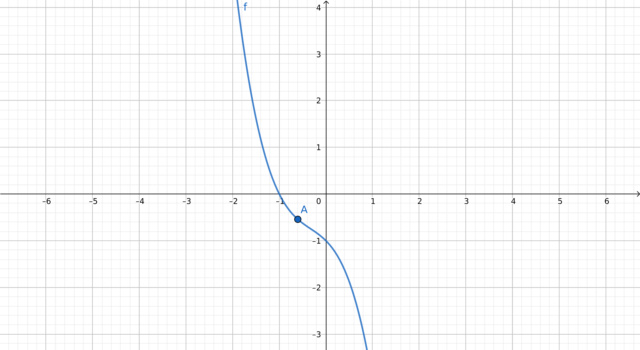
Minha pergunta é: se não há reta tangente ao eixo x, pelo gráfico acho que é isso, esse ponto A (aproximado) é apenas um ponto qualquer? ou é um ponto de inflexão? Fiz a derivada e igualei a zero e deu uma raiz vazia porque a solução não pertence aos reais.

por **Elcioschin** Sáb 11 maio 2019, 14:11

Esta função não tem vértices, onde possam existir retas tangentes paralelas ao eixo x. Logo, não adianta derivar e igualar a derivada a zero.

Agora, no intervalo [-2, 1] existem infinitos pontos onde uma reta pode ser tangente ao gráfico. Neste caso, para um dado ponto P(xP, yP), ao se calcular a derivada no ponto P (fazendo x = xP), obtém-se o valor do coeficiente angular da reta tangente, neste ponto.

Função e pontos críticos

Função e pontos críticos

Re: Função e pontos críticos

Um fórum livre e democrático.