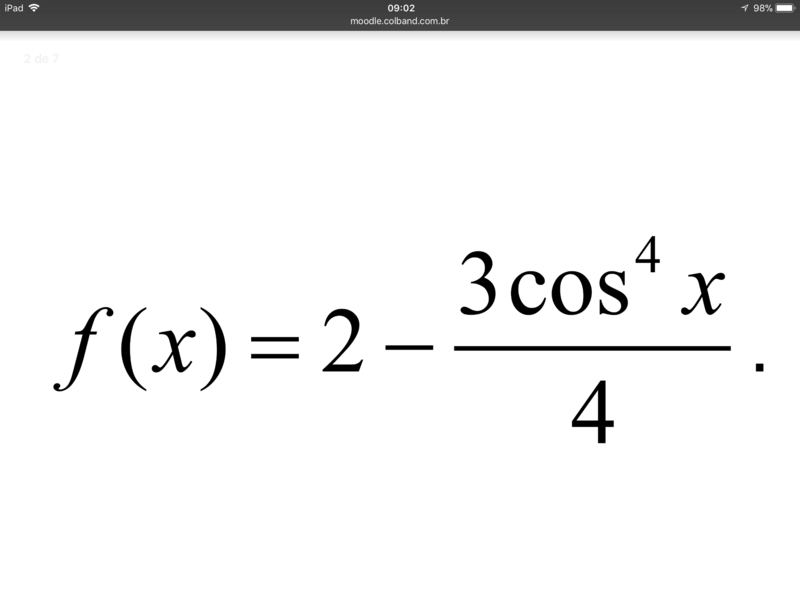FGV Função Trigonométrica
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
sophiab332- Iniciante
- Mensagens : 15
Data de inscrição : 03/04/2018
Idade : 23
Localização : São Paulo, São Paulo, Brasil
 Re: FGV Função Trigonométrica
Re: FGV Função Trigonométrica
Valor máximo ---> x = pi/2 ---> f(x)máx = 2
Valor mínimo ---> x = 0 --> f(x)mín = 2 - 3/4 = 5/4
Valor mínimo ---> x = 0 --> f(x)mín = 2 - 3/4 = 5/4

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: FGV Função Trigonométrica
Re: FGV Função Trigonométrica
Elcioschin, por que o valor mínimo não é x= 3pi/2, já que o cosseno tem valores máximo e mínimo como 1 —> x=pi/2 e -1 —> x=3pi/2?
Enviado pelo Topic'it
Enviado pelo Topic'it
sophiab332- Iniciante
- Mensagens : 15
Data de inscrição : 03/04/2018
Idade : 23
Localização : São Paulo, São Paulo, Brasil
 Re: FGV Função Trigonométrica
Re: FGV Função Trigonométrica
Note que a expressão 3.cos4x/4 esta sendo subtraída de 2
Além disso, como o expoente de cosx é par, a expressão nunca será negativa: ou é positiva ou nula
Quando x = 0 --> cos0 = 1 (valor máximo do cosseno) ---> cos40 = 1 --->
O valor da expressão é máximo, logo o valor de f(x) é mínimo: f(x)mín = 2 - 3/4 --> f(x)mín = 5/4
Quando x = pi/2 ---> cos(pi/2) = 0 ---> A expressão tem o seu valor mínimo logo o valor de f(x) é máximo: f(x)máx = 2 - 0 ---> f(x)máx = 2
Além disso, como o expoente de cosx é par, a expressão nunca será negativa: ou é positiva ou nula
Quando x = 0 --> cos0 = 1 (valor máximo do cosseno) ---> cos40 = 1 --->
O valor da expressão é máximo, logo o valor de f(x) é mínimo: f(x)mín = 2 - 3/4 --> f(x)mín = 5/4
Quando x = pi/2 ---> cos(pi/2) = 0 ---> A expressão tem o seu valor mínimo logo o valor de f(x) é máximo: f(x)máx = 2 - 0 ---> f(x)máx = 2

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Tópicos semelhantes
Tópicos semelhantes» Função trigonométrica
» Função trigonométrica
» função trigonométrica
» FUNÇÃO TRIGONOMÉTRICA
» Função Trigonométrica
» Função trigonométrica
» função trigonométrica
» FUNÇÃO TRIGONOMÉTRICA
» Função Trigonométrica
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos