IME 2014 - Polinômios

O polinômio P(x)=x³-bx²+80x-c possui três raízes inteiras positivas distintas. Sabe-se que duas das raízes do polinômio são divisoras de 80 e que o produto dos divisores positivos de c menores do que c é c² . Qual é o valor de b?

Gabarito:

Começando:

Sejam r, s, t as três raízes positivas distintas

Divisores de 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 ---> r, s divisores de 80

Divisores positivos de c: k, m, n, p .... < c

Briott-Ruffini:

r + s + t = b
r.s + r.t + s.t = 80
r.s.t = c 

k.m.n.p .... = c²

Irei colocar dois teoremas aqui (são tiradas do livro do Rufino), caso você queira a demonstração eu demonstro depois.

Teorema 1: Seja n um inteiro positivo. O número de divisores positivos de n (inclusive 1 e n) indica-se por d(n). Se  é a decomposição canônica do inteiro positivo n > 1, então:


Teorema 2: O produto P(n) dos divisores positivos de um inteiro positivo n > 1 é igual a .

Agora vamos para o exercício.

O enunciado diz que "o produto dos divisores positivos de c menores do que c é c²", perceba que está excluindo o c nessa multiplicação, dessa forma , dai tiramos que d(c) = 6.

d(c) pode ser escrito de duas formas diferentes: d(c) = 6 = (1 + 5) = (1 + 1)(1 + 2), logo c é da forma .

Agora temos dois casos a analisar:

Caso 1: c = p^5
Das relações de Girard (sendo as raízes da equação ) , o que implica , onde 1 ≤ α < β < γ (raízes são distintas), porém α + β + γ ≥ 1 + 2 + 3 = 6;  e p^6 > p^5, o que gera um absurdo. Se uma das raízes for igual a 1, também não irá dar certo (aqui você irá ter que utilizar o fato que duas raízes são divisoras de 80), deixo a você analisar. Portanto o caso 1 não é viável.

Caso 2: 
Lembrando que as raízes são distintas.
. O fator 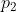 não irá aparecer em pelo menos um dos xi's, se tivermos algum  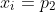as outras duas raízes deverão ser iguais a 1 e p1.p2, pois as raízes devem ser distintas . Se tivermos algum 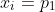, as outras duas raízes deverão ser iguais a 1 e , pois se uma das outras duas raízes fosse igual a 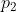 a outra raiz deverá ser também igual a 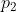, porém as raízes são distintas. Perceba que em todos os casos possíveis temos que ter uma raiz igual a 1. Dessa forma conseguimos encontrar uma raiz, vamos considerar x1 = 1.
Por Girard:
x1.x2 + x1.x3+x2.x3 = 80
x2 + x3 + x2.x3 = 80
x2 + 1 + x3 + x2.x3 = 81
(x2 + 1) + x3(x2 + 1) = 81
(x2 + 1)(x3 + 1) = 81
(x2 + 1)(x3 + 1) = 3.27
x2 + 1 = 3 e x3 + 1 = 27
x2 = 2 e x3 = 26

Por Girard:
x1 + x2 + x3 = b
1 + 2 + 26 = b
b = 29


Obs.: Na hora de analisar os casos, dava para você "chutar" quais eram as duas das raízes do polinômio, já que o enunciado fala que duas delas são divisoras de 80, dai por Girard x1.x2 + x1.x3 + x2.x3 = 80, você substituía ali e via qual que ia dar certo, mas eu fiz do jeito ali de cima que eu acho mais legal.