UFSC 2014 - Polinômios.

por vickbep1901 Dom 27 Set 2020, 16:28

Questão 22 - Prova amarela

Seja p um polinômio de grau 4 dado por p(x) = (x+1)^{4} . Com essa informação, assinale as proposições corretas.

01 - O polinômio p é igual a p(x) = [latex]x^{4} + 4x^{3} + 6x^{2} + 4x + 1[/latex]
02 - O único número real no qual p se anula é x = -1
04 - Se k é um polinômio dado por k(x) = [latex]x^{4} + 4x^{3} + 6x^{2} + 4x + 3[/latex], então o menor valor possível para o polinômio k, quando x varia em todo conjunto dos números reais, é 2.
08 - O coeficiente do termo de expoente 5 do polinômio dado por p(x).(x-1)[latex]^{4}[/latex] é igual a 1.

Alguém poderia me explicar o raciocínio para desenvolver o item 04?

por **Elcioschin** Dom 27 Set 2020, 17:21

k(x) = x⁴ + 4.x³ + 6.x² + 4.x + 3

k(x) = (x⁴ + 4.x³ + 6.x² + 4.x + 1) + 2

k(x) = p(x) + 2 ---> para x = -1 ---> p(x) = 0 ---> k(x) = 2

por **Emanuel Dias** Dom 27 Set 2020, 17:24

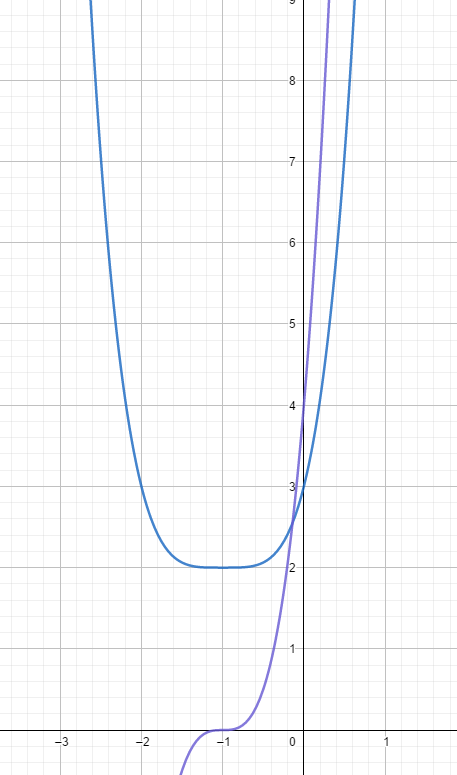
Um outro modo um pouco mais trabalhoso.

Derivando encontramos: 4x³+12x²+12x+4, ou seja:

4(x³+3x²+3x+1)

note que o termo entre parêntese é o desenvolvimento do binômio (x+1)³

Então a derivada da função é 4(x+1)³, o que acontece se derivamos e igualamos a zera? Obtemos os pontos máximos e mínimos da função.

Em x=-1, a função tem máximo ou mínimo, o que podemos deduzir da expressão original? Que ela tem mínimo, pois para o termo x^4, se x vai para menos infinito, a expressão vai para mais infinito, da mesma forma, se x vai para mais infinito, a expressão vai para infinito, então, a função tem minimo em x=-1.

Substituindo na função original, x=-1 implica y=1-4+6-4+3=2.

O mínimo da função ocorre em (-1,2).

Em azul, a função, em roxo a derivada.