Conjuntos Numéricos

I) Se {5; 7} ⊂ A e A ⊂ {5; 6; 7; 8}, então os possíveis conjuntos A
são em números de 4.
II) Supondo A e B conjuntos quaisquer, então sempre temos (A ∩ ∅ )
∪ (B ∪ ∅ ) = A ∪ B.
III) A soma de dois números irracionais pode ser racional.

Das afirmações anteriores:

a) I, II e III são verdadeiras.
b) apenas I e II são verdadeiras.
c) apenas III é verdadeira.
d) apenas II e III são verdadeiras.
e) apenas I e III são verdadeiras.

Favor explicar bem

Na primeira afirmação, chamemos de o conjunto {5;7} de B e o conjunto {5;6;7;8} de C. Lembrando que B está contido em A, então A ''pode'' ser igual a B; A está contido em C, logo A pode ser igual a C. Então, o menor número de elementos de A é 2 e o maior é 4. Os possíveis conjuntos de A {5;7};{5;6;7};{5;7;8} e {5;6;7;8}. Logo a primeira é verdadeira.


Na segunda afirmação, veja que ela diz que A e B são conjuntos quaisquer, logo podemos considerar que A e B são conjuntos não vazios e que A é diferente de B. Veja que e que 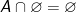, logo teremos 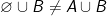. Logo, nem sempre a segunda afirmação é verdadeira.


Na terceira há casos em que a soma de dois números irracionais resulte em um número racional, como a questão diz ''pode ser'', então é verdadeira. Exemplo , zero é um número contido nos racionais.

Valeu pela ajuda abelardo!