Retas e pontos.

por Higor Damacena Sáb 04 Mar 2017, 17:29

Dados A (2, 3) e B (0, 0), vértices do triângulo ABC com área 13√2/2 e sendo BC= 2√13, determine o coeficiente angular da reta BC, sendo C no primeiro quadrante.

Gabarito: mbc= 1/5

por igorrudolf Sáb 04 Mar 2017, 20:17

Olá amigo, boa tarde!

O coeficiente da reta BC, será a tangente do ângulo formado entre essa reta e o eixo x. (ângulo b do desenho)
Observe a figura.

Olhando para a reta AB, e calculando seu coeficiente angular:

m(AB) = ∆y/∆x → m(AB) = 3/2

Ainda sabemos que o coeficiente angular dessa mesma reta AB é igual a tan (a+b).
Portanto tan (a+b) = 3/2 (I)

Agora calculando a medida do segmento AB:
AB² = (∆x)² + (∆y)² → AB² = 13 → AB = √13

Sabemos que área do triângulo ABC pode ser calculada por: 1/2 AB.BC.sin(a), que a área é igual a 13√2/2 e que BC = 2√13, portanto:

$\frac{1}{2}\times \sqrt{13}\times 2\sqrt{13}\times \sin a=\frac{13\sqrt{2}}{2}\rightarrow \sin a=\frac{\sqrt{2}}{2}\therefore a=45°$

Então tan 45° = 1.

Voltando na expressão (I) que encontramos temos:

$\tan (a+b)=\frac{\tan a+\tan b}{1-\tan a\times \tan b}\rightarrow \frac{3}{2}=\frac{1+\tan b}{1-\tan b}$

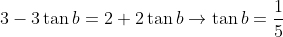
$3-3\tan b=2+2\tan b\rightarrow \tan b=\frac{1}{5}$

por **Medeiros** Sáb 04 Mar 2017, 23:39

Muito bem resolvido. Apenas aproveitando para explicitar porque o ponto C, que deve estar no 1° quadrante, foi colocado num arco abaixo de A.

Teoricamente o ponto C poderia ocupar qualquer região do arco em azul. Neste caso, chamemos de ponto C'. Mas então a maior área possível, indicada no desenho pela posição de C' sobre o eixo y, seria menor que a definida pelo enunciado. Portanto o ponto C deve, obrigatoriamente, estar em alguma posição sobre o arco vermelho.

Uma outra forma de perceber é considerar que o ângulo entre BA e BC deve ser, conforme calculado, alfa=45° e já temos a declividade de BA igual a 3/2, portanto maior que 45°. Neste caso o ponto C resultaria fora do 1° quadrante.