Lado do quadrado
+3
superaks
gilberto97
Julio465
7 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
Lado do quadrado
por Julio465 Seg 16 Jan 2017, 11:06
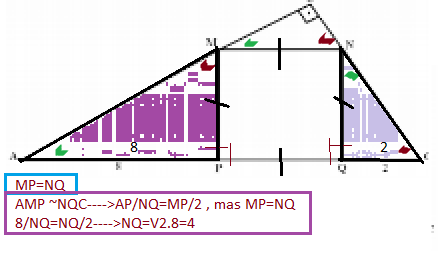
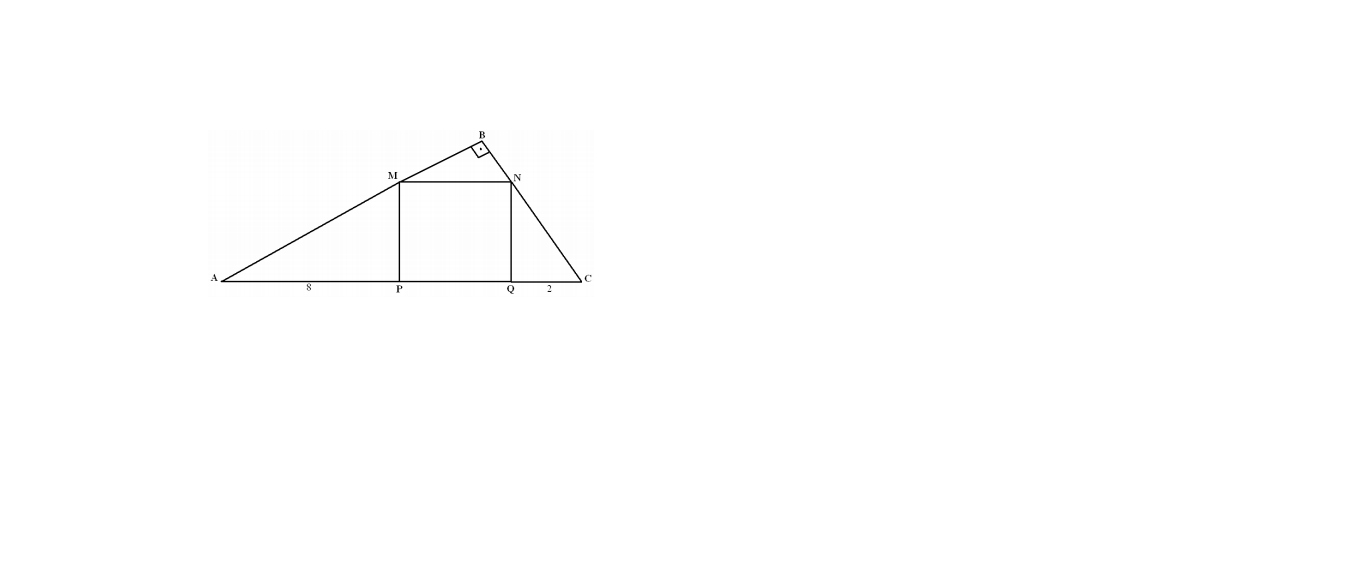
O quadrado de vértices M, N, P e Q está inscrito no triângulo retângulo ABC conforme a figura. Se AP = 8 cm e QC = 2 cm, então o lado do quadrado mede:
(A) 1 cm
(B) 2 cm
(C) 3 cm
(D) 4 cm
(E) 5 cm
Alternativa correta: D
(A) 1 cm
(B) 2 cm
(C) 3 cm
(D) 4 cm
(E) 5 cm
Alternativa correta: D
Julio465- Iniciante
- Mensagens : 2
Data de inscrição : 09/01/2017
Idade : 25
Localização : São Paulo, Brasil
Re: Lado do quadrado
por gilberto97 Seg 16 Jan 2017, 12:41
Bom dia.
No triângulo AMP: tan(MÂP) = L/8
No triângulo NQC: tan(N^CQ) = L/2
Mas MÂP + N^CQ = 90°, ou seja: MÂP = 90° - N^CQ
tan(MÂP) = cotan(N^CQ)
L/8 = 2/L
L² = 16
L = 4 cm
No triângulo AMP: tan(MÂP) = L/8
No triângulo NQC: tan(N^CQ) = L/2
Mas MÂP + N^CQ = 90°, ou seja: MÂP = 90° - N^CQ
tan(MÂP) = cotan(N^CQ)
L/8 = 2/L
L² = 16
L = 4 cm
gilberto97- Fera
- Mensagens : 590
Data de inscrição : 12/03/2014
Idade : 27
Localização : São Luís, Maranhão, Brasil
Re: Lado do quadrado
por Convidado Seg 16 Jan 2017, 12:54
Gilberto esse era o método mais simples de fazer ? eu fiz da seguinte forma x/10=10-x/10=x/2 , achando sim também 4 mas não sei se está correto .gilberto97 escreveu:Bom dia.
No triângulo AMP: tan(MÂP) = L/8
No triângulo NQC: tan(N^CQ) = L/2
Mas MÂP + N^CQ = 90°, ou seja: MÂP = 90° - N^CQ
tan(MÂP) = cotan(N^CQ)
L/8 = 2/L
L² = 16
L = 4 cm
Convidado- Convidado
Julio465- Iniciante
- Mensagens : 2
Data de inscrição : 09/01/2017
Idade : 25
Localização : São Paulo, Brasil
Re: Lado do quadrado
por superaks Ter 17 Jan 2017, 00:01
Olá Gilberto, tudo bem?
Se importa em explicar ou mandar algum link que explique essa conclusão:
MÂP = 90° - N^CQ
tan(MÂP) = cotan(N^CQ)
Grato desde já!
Se importa em explicar ou mandar algum link que explique essa conclusão:
MÂP = 90° - N^CQ
tan(MÂP) = cotan(N^CQ)
Grato desde já!
superaks- Mestre Jedi
- Mensagens : 525
Data de inscrição : 27/06/2016
Idade : 23
Localização : São Paulo, Guarulhos, Brasil
Re: Lado do quadrado
por gilberto97 Ter 17 Jan 2017, 00:56
Boa noite a todos.
Nanzinho, não entendi sua linha de raciocínio. Perdoe-me.
Superaks, você quer a "prova" de que tan(90°-x) = cotan(x). Veja:
tan(90°-x)=sen(90°-x)/cos(90°-x) = cosx/senx = 1/tanx = cotan(x)
Nanzinho, não entendi sua linha de raciocínio. Perdoe-me.
Superaks, você quer a "prova" de que tan(90°-x) = cotan(x). Veja:
tan(90°-x)=sen(90°-x)/cos(90°-x) = cosx/senx = 1/tanx = cotan(x)
gilberto97- Fera
- Mensagens : 590
Data de inscrição : 12/03/2014
Idade : 27
Localização : São Luís, Maranhão, Brasil
Re: Lado do quadrado
por Convidado Ter 17 Jan 2017, 08:10
Também por semelhança , mas creio que está errado .gilberto97 escreveu:Boa noite a todos.
Nanzinho, não entendi sua linha de raciocínio. Perdoe-me.
Superaks, você quer a "prova" de que tan(90°-x) = cotan(x). Veja:
tan(90°-x)=sen(90°-x)/cos(90°-x) = cosx/senx = 1/tanx = cotan(x)
Convidado- Convidado
Re: Lado do quadrado
por Elcioschin Ter 17 Jan 2017, 10:06
A solução do nanzinho é a mesma do gilberto97
A única diferença é que o gilberto 97 provou que os ângulos são iguais e por isto vale a semelhança.
Vou mostrar de modo similar
Seja θ o ângulo BÂC = MÂP
Como ABC é retângulo ---> A^CB = 90º - θ
Como NQC também é um triângulo retângulo ---> C^QN = θ
Triângulos APM e CQN são semelhantes:
tgMÂP = MP/AP---> tgθ = L/8
tgC^NQ= CQ/NQ ---> tgθ = 2/L
L/8 = 2/L ---> L = 4
A única diferença é que o gilberto 97 provou que os ângulos são iguais e por isto vale a semelhança.
Vou mostrar de modo similar
Seja θ o ângulo BÂC = MÂP
Como ABC é retângulo ---> A^CB = 90º - θ
Como NQC também é um triângulo retângulo ---> C^QN = θ
Triângulos APM e CQN são semelhantes:
tgMÂP = MP/AP---> tgθ = L/8
tgC^NQ= CQ/NQ ---> tgθ = 2/L
L/8 = 2/L ---> L = 4
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Lado do quadrado
por Medeiros Qua 18 Jan 2017, 02:50
Outro modo.
Seccionamos o triângulo pelos lados verticais do quadrado, jogamos fora a parte do meio e unimos as duas extremidades; ficamos com um novo triângulo retângulo cuja altura ref. à hipotenusa é o próprio lado do quadrado; a vantagem é que neste (novo) conhecemos as projeções sobre a hipotenusa.
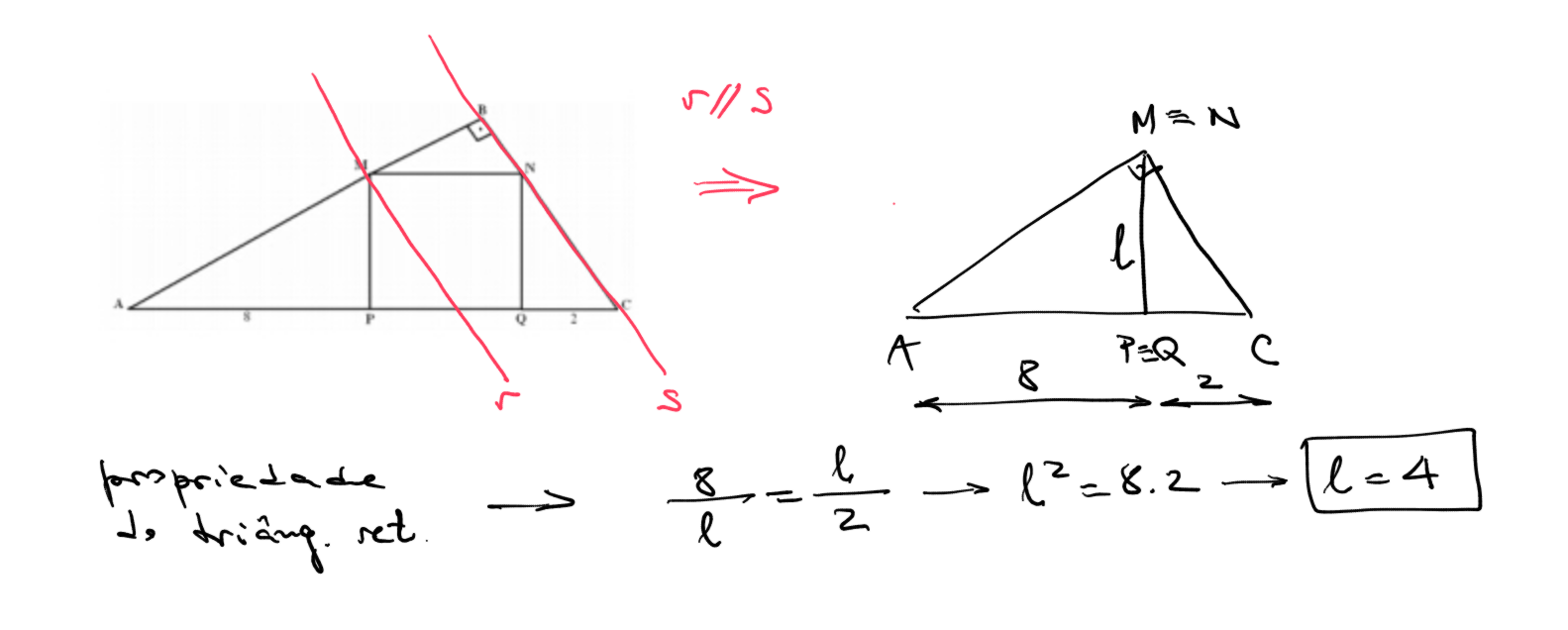
Seccionamos o triângulo pelos lados verticais do quadrado, jogamos fora a parte do meio e unimos as duas extremidades; ficamos com um novo triângulo retângulo cuja altura ref. à hipotenusa é o próprio lado do quadrado; a vantagem é que neste (novo) conhecemos as projeções sobre a hipotenusa.
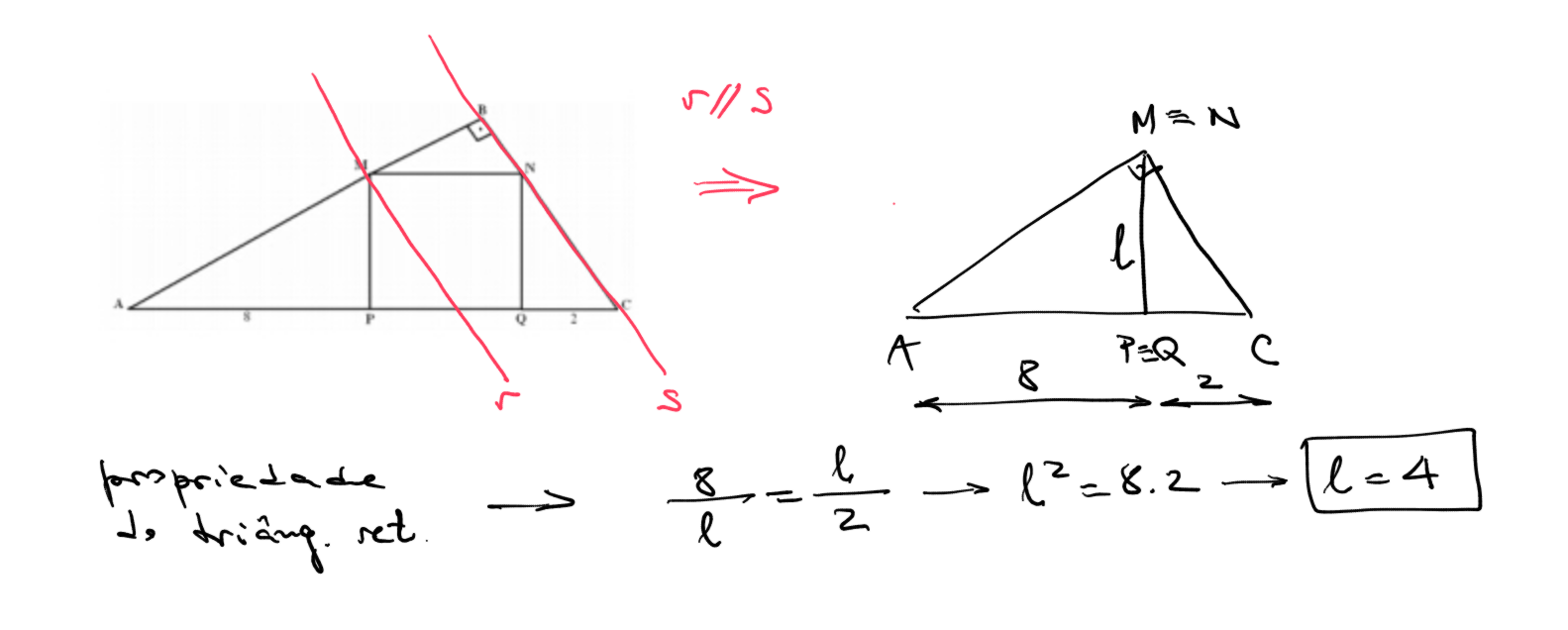
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Página 1 de 2 • 1, 2
Tópicos semelhantesPágina 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
