Exercício da Fuvest
5 participantes
Página 2 de 2
Página 2 de 2 •  1, 2
1, 2
 Exercício da Fuvest
Exercício da Fuvest
Relembrando a primeira mensagem :
Na figura a seguir, a reta r tem equação y=2√2x + 1 no plano cartesiano 0xy. Além disso, os pontos B0,B1,B2,B3 estão na reta r, sendo B0=(0,1). Os pontos A0,A1,A2,A3 estão no eixo 0x, com A0=0=(0,0). O ponto Di pertence ao segmento B0B1,B1B2,B2B3 são paralelos ao eixo 0x, e a distancia entre Bi e Bi+1 é igua a 9, para 0<=i<=2.
a)Determine as abscissas de A1,A2,A3.
b)Sendo Ri, o retângulo de base AiAi+1 e altura Ai+1Di+1, para 0<=i<=2, Calcule a soma das áreas dos retângulos R0,R1 e R2.
a - 3,6 e 9
b - 9+54√2
Na figura a seguir, a reta r tem equação y=2√2x + 1 no plano cartesiano 0xy. Além disso, os pontos B0,B1,B2,B3 estão na reta r, sendo B0=(0,1). Os pontos A0,A1,A2,A3 estão no eixo 0x, com A0=0=(0,0). O ponto Di pertence ao segmento B0B1,B1B2,B2B3 são paralelos ao eixo 0x, e a distancia entre Bi e Bi+1 é igua a 9, para 0<=i<=2.
a)Determine as abscissas de A1,A2,A3.
b)Sendo Ri, o retângulo de base AiAi+1 e altura Ai+1Di+1, para 0<=i<=2, Calcule a soma das áreas dos retângulos R0,R1 e R2.
a - 3,6 e 9
b - 9+54√2
Evandro A. T. Borsato- Recebeu o sabre de luz

- Mensagens : 173
Data de inscrição : 04/12/2016
Idade : 29
Localização : São José Dos Campos,SP,BR
 Re: Exercício da Fuvest
Re: Exercício da Fuvest
cosθ = 1/3 ---> senθ = 2.√2/3
D2B1 = BoB1.senθ ---> D2B1 = 9.2.√2/3 ---> D2B1 = 6.√2
D3B2 = D2B1 ---> D3B2 = 6.√2
Área de A0B0D2A3 = A0A1.A0B0 = 3.1 = 3
Área de A1B1D3A2 = A1A2.A1B1 = A1A2(A1D2 + D2B1) = 3.(1 + 6.√2) = 3 + 18√2
Área de A2B2D4A3 = A2A3.A2B2 = 3.(1 + 6.√2 + 6.√2) = 3 + 36√2
Soma das áreas dos três retângulos = 3 + (3 + 18√2) + (3 + 36.√2) = 9 + 54.√2
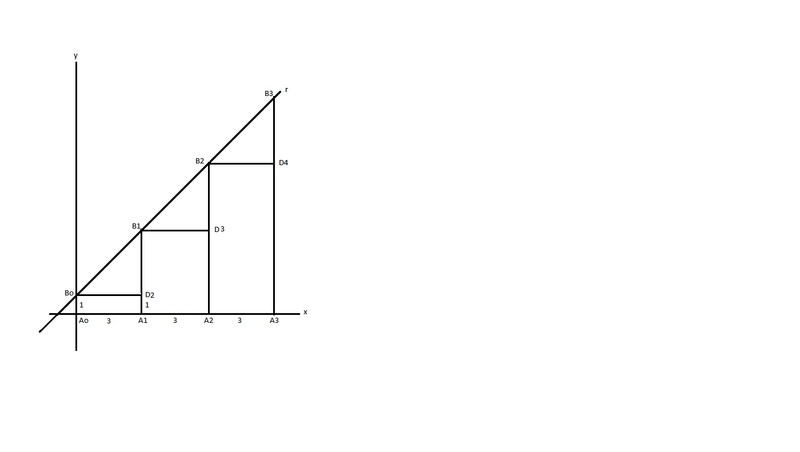
D2B1 = BoB1.senθ ---> D2B1 = 9.2.√2/3 ---> D2B1 = 6.√2
D3B2 = D2B1 ---> D3B2 = 6.√2
Área de A0B0D2A3 = A0A1.A0B0 = 3.1 = 3
Área de A1B1D3A2 = A1A2.A1B1 = A1A2(A1D2 + D2B1) = 3.(1 + 6.√2) = 3 + 18√2
Área de A2B2D4A3 = A2A3.A2B2 = 3.(1 + 6.√2 + 6.√2) = 3 + 36√2
Soma das áreas dos três retângulos = 3 + (3 + 18√2) + (3 + 36.√2) = 9 + 54.√2
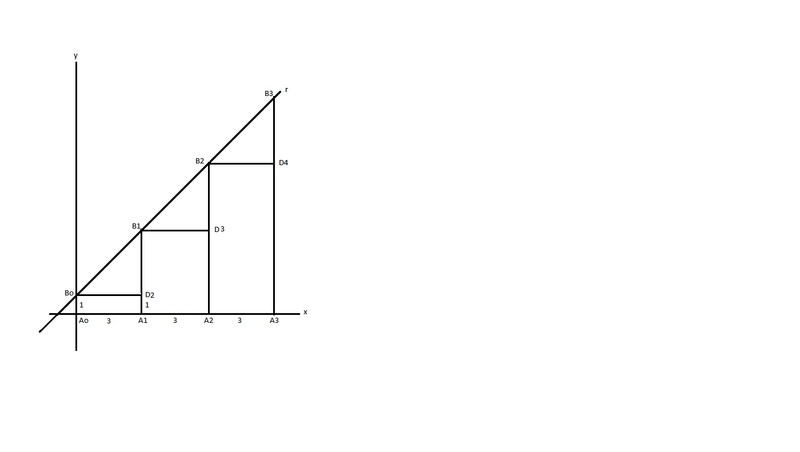

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 2 de 2 •  1, 2
1, 2
 Tópicos semelhantes
Tópicos semelhantes» Exercicio da Fuvest
» [Fuvest exercício]
» [Exercício Fuvest dissertativo]
» Exercício fuvest - sp 2015
» Dúvida - Exercício Fuvest
» [Fuvest exercício]
» [Exercício Fuvest dissertativo]
» Exercício fuvest - sp 2015
» Dúvida - Exercício Fuvest
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












