MHs questão da uesb sem adaptação

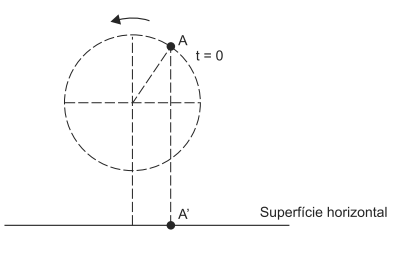
A figura representa a posição inicial de uma partícula que descreve movimento circular uniforme em um plano vertical, com frequência de 240rpm, sendo iluminada pela luz do Sol a pino. Sabendo-se que a linha vertical que liga a posição inicial da partícula e que a sua sombra projetada na superfície horizontal passa exatamente no meio do raio da trajetória que mede 1,0m, é correto afirmar que a função horária do movimento descrito pela sombra A,no SI, é igual a




gab 05

Note que todas as alternativas apresentam frequência angular diferente, ou seja, a determinação da frequência apenas já nos dá a resposta correta. Este tipo de raciocínio é muito útil para salvar tempo em provas. Mas, aqui, resolverei a questão por completo.

f = 240 rpm = 4 rps = 4 hz

w = 2*pi*f --> w = 8pi 

A posição inicial nos permitirá determinar a fase do movimento.

Marque na circunferência o centro O e um ponto P tal que P seja a intercessão entre o segmento AA' e a reta horizontal que parte de O.

Sabendo que no instante inicial a sombra projetada passa exatamente pelo centro do raio de 1 m, podemos inferir que nesse instante OP = 1/2, e o ângulo descrito é a fase, já que é o instante inicial. Note que podemos determinar este ângulo, pois um dos catetos é OP e a hipotenusa é OA:

OP/OA = cos(phi) --> cos(phi) = 1/2 --> phi = pi/3.

Como o raio é 1, a amplitude é 1, logo:

x(t) = A*cos(wt + phi)

x(t) = cos(8pi*t + pi/3)

Abraços