Máximos e Mínimos em FunçãoQuadrática
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Máximos e Mínimos em FunçãoQuadrática
Máximos e Mínimos em FunçãoQuadrática
Boa tarde, gostaria de um esclarecimento no exercício abaixo:
No triângulo retângulo representado abaixo cada um dos catetos mede 3cm. Considere um ponto C da hipotenusa e o retângulo ABCD, sendo x a medida de AD
Determine:
a) a área S do retângulo ABCD em função de x;
b) para que valor(es) de x se tem S ≤ 1,25cm²
Segue a resolução dada como correta:
a) Chamando CD de h teremos S = x . h
Mas, AEF ~DCF
Assim, h = 3 - x e S = x(3 – x) → Resposta: 3x – x² , 0 ≤ x ≤ 3
b) 0 < S ≤ 1,25
0 < 3x – x² ≤ 1,25
–x² + 3x +5/4 ≤ 0 → Resolvendo teremos x ≤ 1/2 ou x x ≥ 5/2 (I)
Por outro lado,
3x – x² > 0 → x² – 3x < 0 → x(x – 3) < 0 Resolvendo teremos 0 < x < 3 (II)
Interseção de (I) com (II) teremos a Resposta 0 < x ≤ 1/2 ou 5/2 ≤ x < 3
Minha dúvida é a seguinte: por que na letra a), é permitido ter S = 0 visto que a resposta inclui as raízes da função 0 e 3 na resposta (0≤ x ≤ 3) e na letra b não se permite S = 0 visto que as raízes não são inclusas (0 < x < 3)? Desde já grato pela atenção.

No triângulo retângulo representado abaixo cada um dos catetos mede 3cm. Considere um ponto C da hipotenusa e o retângulo ABCD, sendo x a medida de AD
Determine:
a) a área S do retângulo ABCD em função de x;
b) para que valor(es) de x se tem S ≤ 1,25cm²
Segue a resolução dada como correta:
a) Chamando CD de h teremos S = x . h
Mas, AEF ~DCF
Assim, h = 3 - x e S = x(3 – x) → Resposta: 3x – x² , 0 ≤ x ≤ 3
b) 0 < S ≤ 1,25
0 < 3x – x² ≤ 1,25
–x² + 3x +5/4 ≤ 0 → Resolvendo teremos x ≤ 1/2 ou x x ≥ 5/2 (I)
Por outro lado,
3x – x² > 0 → x² – 3x < 0 → x(x – 3) < 0 Resolvendo teremos 0 < x < 3 (II)
Interseção de (I) com (II) teremos a Resposta 0 < x ≤ 1/2 ou 5/2 ≤ x < 3
Minha dúvida é a seguinte: por que na letra a), é permitido ter S = 0 visto que a resposta inclui as raízes da função 0 e 3 na resposta (0≤ x ≤ 3) e na letra b não se permite S = 0 visto que as raízes não são inclusas (0 < x < 3)? Desde já grato pela atenção.

petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
 Re: Máximos e Mínimos em FunçãoQuadrática
Re: Máximos e Mínimos em FunçãoQuadrática
Também não vejo razão para isso. Obviamente S=0 -> S≤1,25.petras escreveu:Minha dúvida é a seguinte: por que na letra a), é permitido ter S = 0 visto que a resposta inclui as raízes da função 0 e 3 na resposta (0≤ x ≤ 3) e na letra b não se permite S = 0 visto que as raízes não são inclusas (0 < x < 3)? Desde já grato pela atenção.
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Máximos e Mínimos em FunçãoQuadrática
Re: Máximos e Mínimos em FunçãoQuadrática
O correto na letra a) não seria 0 < x < 3 pois se considerarmos 0 e 3 como solução, não haveria sentido pois a área seria 0?
____________________________________________

_______________________________
"Ex nihilo nihil fit"
petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
 Re: Máximos e Mínimos em FunçãoQuadrática
Re: Máximos e Mínimos em FunçãoQuadrática
Acho que seu gab da A) está errado, no meu livro do Bernoulli o gab é
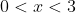 .
.
Êxodo Sousa- Iniciante
- Mensagens : 42
Data de inscrição : 25/08/2020
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












