Máximos e mínimos

por viniciusp10 Sáb 05 Out 2019, 09:03

Uma viga de aço (segmento AB) de comprimento 64m está sendo transportada através de um corredor com 8m de largura. No fim do corredor, há uma curva, em ângulo reto, que leva a um corredor com L m de largura. Qual é o menor valor de L, de tal modo que essa viga possa ser transportada horizontalmente em torno do canto?

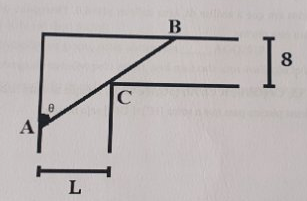
Máximos e mínimos File

Obs: O mínimo valor de L, que satisfaz a situação dada, é obtido quando temos, necessariamente, a configuração da figura acima. Logo, devemos procurar o maior valor de L para que o desenho acima ocorra, ou seja, as extremidades A e B da viga devem enconstar ao mesmo tempo nas paredes dos corredores, e um de seus pontos interiores, na quina C.

Preciso que seja resolvido usando derivadas.

por **Elcioschin** Sáb 05 Out 2019, 16:40

Seja D o vértice da parede externa que contém A e B
Sejam M e N os pés das perpendiculares de C sobre as paredes AD e BD
Seja AM = y e BN = x

DM = CN = 8 ---> DN = CM = L

tgθ = BD/AD = BN/CN ---> (L + x)/(8 + y) = x/8 ---> x.y = 8.L ---> y = 8.L/x ---> I

AC² = y² + L² ---> II
BC² = x² + 8² ---> BC² = x² + 64 ---> II

AC + BC = 64 ---> III

Tente agora completar

Máximos e mínimos

Máximos e mínimos

Re: Máximos e mínimos

Um fórum livre e democrático.