Equação trigonometria UEL
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 Equação trigonometria UEL
Equação trigonometria UEL
UFL) O conjunto-solução da equação senx=sen2x, no universo U= [0,2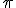 ], é:
], é:
Resposta: {0,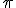 /3 ,
/3 , 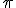 , 5
, 5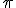 /3, 2
/3, 2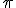 }
}
Resposta: {0,
victor H- Padawan

- Mensagens : 72
Data de inscrição : 17/12/2014
Idade : 24
Localização : salvador
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
sen x = sen 2x
sen x = sen (x + x)
sen x = 2. senx . cosx
Primeira solução: senx= 0 --> x = 0 ou x =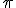 ou x = 2
ou x = 2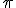 (ambos os lados resultaram em zero)
(ambos os lados resultaram em zero)
Soluções posteriores:
Dividindo ambos os lados por sen x:
1 = 2 cos x
cos x = 1/2
x =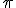 /3 ou x = 5
/3 ou x = 5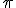 /3
/3
sen x = sen (x + x)
sen x = 2. senx . cosx
Primeira solução: senx= 0 --> x = 0 ou x =
Soluções posteriores:
Dividindo ambos os lados por sen x:
1 = 2 cos x
cos x = 1/2
x =

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
Eu não entendi esse primeira resolução, onde senx=0 etc.. tem alguma explicação teórica? Pq igualar direto àzero?
victor H- Padawan

- Mensagens : 72
Data de inscrição : 17/12/2014
Idade : 24
Localização : salvador
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
E por que dividindo-se os dois lados da equação por senx, perde-se as solução onde senx=0?
victor H- Padawan

- Mensagens : 72
Data de inscrição : 17/12/2014
Idade : 24
Localização : salvador
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
Boa pergunta!!
Percebeu que quando dividimos os dois lados por sen x, excluímos completamente essa expressão da fórmula?
Isso ocorreu porque todos os membros da equação tinha em sua composição o fator sen x.
Observe:
8a = ab
Quanto vale b?
b = 8 independentemente de "a".
Porém, quando a = 0, a equação será verdadeira independente do valor de "b".
Voltando para nossa expressão:
senx = 2cosx. senx
Caso o sen x seja igual a zero, teremos: 0 = 2.cosx.0
0 = 0
O que é verdadeiro, independente do valor do cosseno. Mas dividindo por sen x, descobriremos o valor do cosseno para que independente do valor do senx a igualdade se mantenha.
Foi um pouco subjetivo, mas você compreendeu?
Percebeu que quando dividimos os dois lados por sen x, excluímos completamente essa expressão da fórmula?
Isso ocorreu porque todos os membros da equação tinha em sua composição o fator sen x.
Observe:
8a = ab
Quanto vale b?
b = 8 independentemente de "a".
Porém, quando a = 0, a equação será verdadeira independente do valor de "b".
Voltando para nossa expressão:
senx = 2cosx. senx
Caso o sen x seja igual a zero, teremos: 0 = 2.cosx.0
0 = 0
O que é verdadeiro, independente do valor do cosseno. Mas dividindo por sen x, descobriremos o valor do cosseno para que independente do valor do senx a igualdade se mantenha.
Foi um pouco subjetivo, mas você compreendeu?

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
Simm, eu entendi sua explicação, foi perfeita! A univ coisa que não entendi, é como ter a "sacada"de igualar logo de cara o senx = 0. É algum procedimento "padrao"? Toda vez que tiver alguma equação desse tipo, uma das soluções será essa (senx=0)?
victor H- Padawan

- Mensagens : 72
Data de inscrição : 17/12/2014
Idade : 24
Localização : salvador
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
Esse procedimento é em decorrência de uma fatoração. Observe:victor H escreveu:Simm, eu entendi sua explicação, foi perfeita! A univ coisa que não entendi, é como ter a "sacada"de igualar logo de cara o senx = 0. É algum procedimento "padrao"? Toda vez que tiver alguma equação desse tipo, uma das soluções será essa (senx=0)?
sen x = 2. senx . cosx
sen x - 2senx. cosx = 0 (apenas "passei" para o outro lado subtraindo)
Colocando o sen x em evidência (técnica de fatoração):
senx (1 - 2cosx) = 0
Daí, para o produto entre duas "coisas" resultar em 0, um dos fatores precisa ser obrigatoriamente 0.
Com isso, ou senx =0 (solução 1) ou 1- 2cosx = 0 (solução 2)
Percebeu?
É um procedimento automático baseado em fatoração.
Vou dar um exemplo com uma equação do segundo grau:
Quais são as raízes da expressão a seguir?
x² + x = 0
Você pode resolver por Bhaskara, ou simplesmente fatorar, até porque, a fórmula de Bhaskara não é nada mais nada menos do que uma fatoração.
Para fatorar, basta você perceber que todos os membros tem um fator x. Observe:
x.x + 1.x = 0.x
O último podemos suprimir porque todo número vezes zero resulta em zero.
Com isso:
x.x + 1.x = 0
Colocando em evidência:
x(x+ 1) = 0
Portanto, ou x = 0 ou x + 1 = 0 -> x = -1
Se você simplesmente "cortasse" o x perderia uma solução, o que não pode acontecer. É muito importante você sempre fazer esse procedimento como algo automático para não eliminar soluções sem querer!

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Re: Equação trigonometria UEL
Re: Equação trigonometria UEL
Fantástico!! Agora sim consegui entender tudo! Esclarecimento total! Muito obrigado mesmo, não imagina o quanto me ajudou. Ficou tudo claro na minha cabeça finalmente hahah. Obrigado mesmo!!! Abraços
victor H- Padawan

- Mensagens : 72
Data de inscrição : 17/12/2014
Idade : 24
Localização : salvador
 Tópicos semelhantes
Tópicos semelhantes» Equação-(trigonometria)
» Trigonometria equacao
» Trigonometria - Equação
» Equação trigonometria
» Equação trigonometria
» Trigonometria equacao
» Trigonometria - Equação
» Equação trigonometria
» Equação trigonometria
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












