Agilidade com Gráficos de função
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Agilidade com Gráficos de função
Agilidade com Gráficos de função
Boa noite pessoal, comecei o estudo das funções já faz algum tempo, porém apenas à pouco tempo descobri algumas técnicas de fácil demonstração e que acho que podem ser do interesse da maioria para o melhor entendimento de gráficos de funções,além de agilizar os exercícios de gráficos de funções. O tópico não aparece bem explicado ao menos no meu atual volume de funções do Iezzi, e só vi uma abordagem um pouco mais detalhada do tema em pré - cálculo. Sem mais delongas:
Suponhamos conhecido o gráfico de uma função y = f(x):
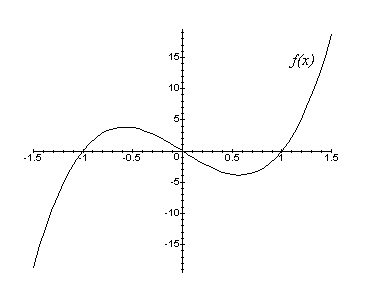 Então, a partir de operações simples (translações, reflexões, ...) no gráfico de f, é possível construirmos facilmente os gráficos das seguintes funções:
Então, a partir de operações simples (translações, reflexões, ...) no gráfico de f, é possível construirmos facilmente os gráficos das seguintes funções:
[list="color: rgb(0, 0, 0); font-family: arial, helvetica; font-size: medium; background-color: rgb(255, 255, 255);"]
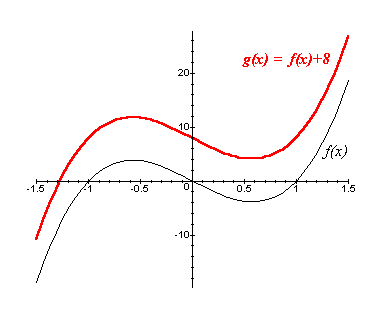
[*]g(x) = f(x) + a, a > 0
Neste caso, o gráfico de g pode ser construído através do deslocamento (translação) de "a" unidades para cima do gráfico de f.
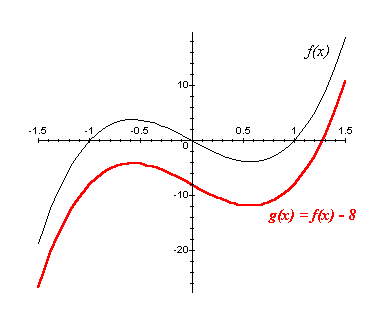
[*]g(x) = f(x) - a, a > 0
O gráfico de g pode ser construído através do deslocamento de "a" unidades para baixo do gráfico de f.
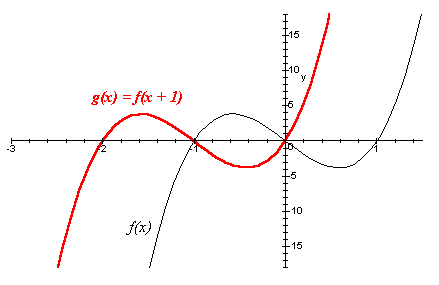
[*]g(x) = f(x + a), a > 0
O gráfico de g pode ser construído através do deslocamento de "a" unidades para a esquerda do gráfico de f.
[*]g(x) = f(x - a), a > 0
O gráfico de g pode ser construído através do deslocamento de "a" unidades para a direita do gráfico de f.

[*]g(x) = -f(x)
O gráfico de g pode ser construído através da reflexão em torno do eixo dos x do gráfico de f, ou seja, os pontos do gráfico de f que estiverem abaixo do eixo x são refletidos para cima e os que estiverem acima do eixo x são refletidos para baixo.
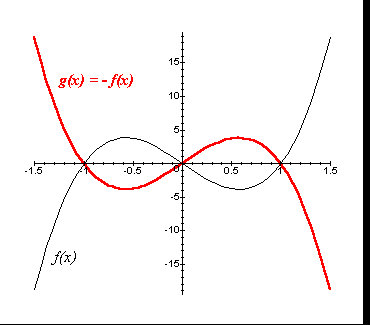
[*]g(x) = f(-x)
O gráfico de g pode ser construído através da reflexão em torno do eixo dos y do gráfico de f, ou seja, os pontos do gráfico de f que estiverem à esquerda do eixo y são refletidos para a direita e os que estiverem à direita do eixo y são refletidos para a esquerda.
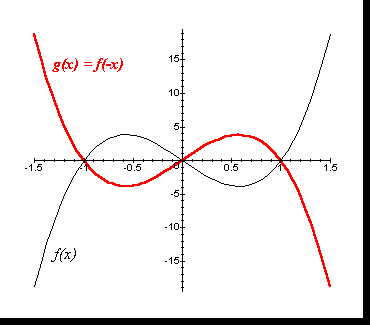
[*]g(x) = |f(x)|
O gráfico de g pode ser construído através da reflexão em torno do eixo dos x da parte do gráfico de f que estiver abaixo desse eixo. A parte do gráfico de f que estiver acima do eixo dos x faz parte do gráfico de g sem modificações.
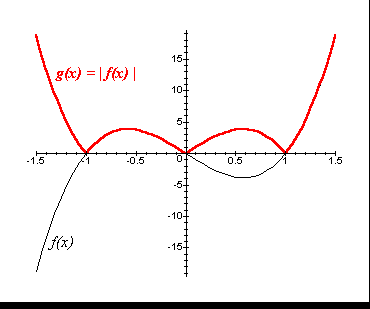
[*]g(x) = f(a x), a < 1
O gráfico de g pode ser construído através de um alongamento na direção horizontal do gráfico de f:

[*]g(x) = f(a x), a > 1
O gráfico de g pode ser construído através de um encolhimento na direção horizontal do gráfico de f:
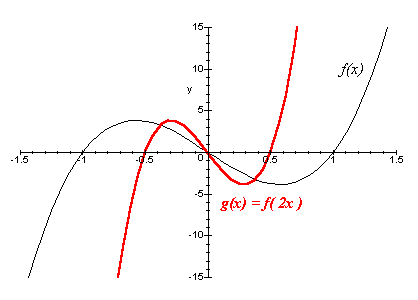
[*]g(x) = a f(x), a < 1
O gráfico de g pode ser construído através de um encolhimento na direção vertical do gráfico de f:
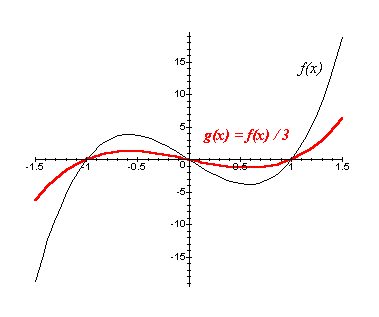
[*]g(x) = a f(x), a > 1
O gráfico de g pode ser construído através de um alongamento na direção vertical do gráfico de f:
[/list]
Suponhamos conhecido o gráfico de uma função y = f(x):
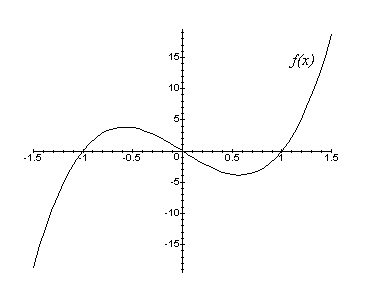
[list="color: rgb(0, 0, 0); font-family: arial, helvetica; font-size: medium; background-color: rgb(255, 255, 255);"]
[*]g(x) = f(x) + a, a > 0
Neste caso, o gráfico de g pode ser construído através do deslocamento (translação) de "a" unidades para cima do gráfico de f.

[*]g(x) = f(x) - a, a > 0
O gráfico de g pode ser construído através do deslocamento de "a" unidades para baixo do gráfico de f.

[*]g(x) = f(x + a), a > 0
O gráfico de g pode ser construído através do deslocamento de "a" unidades para a esquerda do gráfico de f.

[*]g(x) = f(x - a), a > 0
O gráfico de g pode ser construído através do deslocamento de "a" unidades para a direita do gráfico de f.

[*]g(x) = -f(x)
O gráfico de g pode ser construído através da reflexão em torno do eixo dos x do gráfico de f, ou seja, os pontos do gráfico de f que estiverem abaixo do eixo x são refletidos para cima e os que estiverem acima do eixo x são refletidos para baixo.

[*]g(x) = f(-x)
O gráfico de g pode ser construído através da reflexão em torno do eixo dos y do gráfico de f, ou seja, os pontos do gráfico de f que estiverem à esquerda do eixo y são refletidos para a direita e os que estiverem à direita do eixo y são refletidos para a esquerda.

[*]g(x) = |f(x)|
O gráfico de g pode ser construído através da reflexão em torno do eixo dos x da parte do gráfico de f que estiver abaixo desse eixo. A parte do gráfico de f que estiver acima do eixo dos x faz parte do gráfico de g sem modificações.

[*]g(x) = f(a x), a < 1
O gráfico de g pode ser construído através de um alongamento na direção horizontal do gráfico de f:

[*]g(x) = f(a x), a > 1
O gráfico de g pode ser construído através de um encolhimento na direção horizontal do gráfico de f:

[*]g(x) = a f(x), a < 1
O gráfico de g pode ser construído através de um encolhimento na direção vertical do gráfico de f:

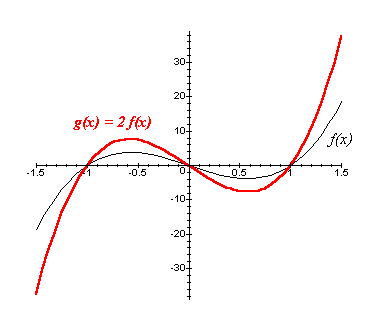
[*]g(x) = a f(x), a > 1
O gráfico de g pode ser construído através de um alongamento na direção vertical do gráfico de f:

[/list]
Créditos à UFPB, pela ótima explicação, que foi de onde copiei o conteúdo do post. aqui fica o link para quem quiser conferir o original
Última edição por TOMASNPB em Dom 14 Fev 2016, 19:17, editado 1 vez(es) (Motivo da edição : editado por alguns desvios da norma padrão)

TOMASNPB- Padawan

- Mensagens : 59
Data de inscrição : 15/12/2014
Idade : 25
Localização : Recife,PE,BRASIL
 Re: Agilidade com Gráficos de função
Re: Agilidade com Gráficos de função
Seria bom recolocar as imagens 

Augusto H.- Mestre Jedi

- Mensagens : 509
Data de inscrição : 22/03/2017
Idade : 25
Localização : Porto Alegre
 Re: Agilidade com Gráficos de função
Re: Agilidade com Gráficos de função
Não há como re-upar as imagens?
ivanginato23- Recebeu o sabre de luz

- Mensagens : 121
Data de inscrição : 20/03/2017
Idade : 25
Localização : São Paulo
 Re: Agilidade com Gráficos de função
Re: Agilidade com Gráficos de função
Reparem que ao final de sua mensagem ele cedeu os créditos à UFPB, e no trecho ''aqui fica o link [...]'' há um código sobre ele que leva ao arquivo original. Arquivo esse que é exatamente o do tópico.

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Os gráficos da função...
» graficos de função
» Gráficos e função
» Os gráficos da função 1 Grau
» Função - Gráficos
» graficos de função
» Gráficos e função
» Os gráficos da função 1 Grau
» Função - Gráficos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












