Lugar Geométrico da Escada

Uma escada encontra-se inicialmente estática na vertical contra uma parede. Sua extremidade inferior é golpeada fazendo com que a escada deslize para baixo. Assuma que a extremidade inferior mantenha contato com o chão e a superior com a parede. Descreva o lugar geométrico do envelope das posições da escada. 

Não tenho o gabarito. Meu professor vai dar a resposta quarta-feira.

Definição do meu professor (a dica que ele deu): Envelope é a posição de todos os pontos, em uma inclinação A da escada, que não mudam para uma pequena mudança de A.

Considere que a escada AB tenha 5 m de comprimento: inicialmente seu ponto médio M está a 2,5 m de altura.

Desenhe um sistema xOy (y é a parede e x o solo) e marque os seguintes pontos:

A(0; 5) e B(0; 0) e M(0; 2,5) ---> Escada em pé na parede

A'(0; 4), B'(3; 0) e M'(1,5 ; 2,0) ---> AA' = 1 e OB' = 3 ---> Escada escorregou 1 m (na vertical) e 3 m (na horizontal)

A"(0; 3), B"(4; 0) e M"(2,0 ; 1,5) ---> AA" = 2 e OB" = 4 ---> Idem 2 e 4

A'"(0, 0), B'"(5, 0) e M'"(2,5 ; 0) ---> Escada no chão

Trace a curva M - M' - M" - M'" ---<> circunferência com centro na origem e raio = 2,5 m --> x² + y² = 2,5²

Também vi isso, Élcio, mas essa é a curva do ponto médio da escada e assim fica muito fácil.

Não me ficou claro o que ele quis dizer com "lugar geométrico dos pontos da curva tangente a escada", mas acho que seria a curva vermelha no desenho. Nele, além do percurso do ponto médio (circunferência laranja), tomei também o percurso de três pontos acima e três abaixo desse ponto.

Observe a figura na qual está representada a escada em dois instantes distintos. No primeiro o ângulo que a escada faz com o solo é  \theta+d\theta e no segundo é apenas  \theta . Fazendo o comprimento da escada como igual a 1, podemos fazer alguns cálculos.



Trace uma perpendicular em B que passe por CD no ponto E. Logo  \Delta ACP\sim \Delta BEP . Pela figura é fácil concluir que

 AC = sen(\theta+d\theta)-sen(\theta)

Saiba que  cos(\theta)=\frac{sen(\theta+d\theta)-sen(\theta)}{d\theta} . Temos então...

 AC\approx cos(\theta)d\theta

Analogamente, você pode concluir que

 BD=-cos(\theta+d\theta)+cos(\theta)\approx sen(\theta)d\theta

Podemos calcular BE, já que  BE=BD.tan(\theta) . Substituindo BD:

 BE\approx tan(\theta)sen(\theta)d\theta

A razão de semelhança entre os triângulos ACP e BEP pode ser obtida pela razão entre AC e BE, que já conhecemos. 

 \frac{AC}{BE}=k\approx \frac{cos(\theta)}{tan(\theta)sen(\theta)}=\frac{cos^{2}(\theta)}{sen^{2}(\theta)}

Desta mesma semelhança:

 \frac{AP}{BP}=k

AP = 1 - PB    \therefore  

 PB=\frac{1}{1+k}

Trace outra perpendicular a OD que toque OB em F, mas dessa vez passando por P. Note a semelhança dos triângulos AOB e PFB. Então:

 \frac{OB}{FB}=\frac{1}{PB}

 FB = OB.PB

A coordenada x de P pode ser calculada pela diferença OB - FB.

 x_{P}=OB-FB=OB(1-PB)=\frac{k}{1+k}OB

Olhe novamente para a figura, desta vez para o triângulo AOB. Perceba que

 OB = cos(\theta+d\theta)\approx cos(\theta)

Portanto:

 x_{P}=\frac{cos^{2}(\theta)}{sen^{2}(\theta)+cos^{2}(\theta)}cos(\theta)=cos^{3}(\theta)

Falta calcular y. Para isso, trace outra perpendicular, dessa vez em AO, passando por P. O ponto de intersecção chame de G. É fácil ver que  PG=x_{p}=cos^{3}(\theta) . Atente também para o fato de que os ângulos  \widehat{APG} e  \widehat{PBO} são iguais. Conclui-se que 

 \frac{AG}{GP}=tan(\theta+d\theta)\approx tan(\theta)

Como y = AO - AG, temos que

 y_{P}=AO-GP.tan(\theta)

 y_{P}=sen(\theta)-sen(\theta)cos^{2}(\theta)\, \, \, \, \, \, \, \, \, \left ( \because GP=cos^{3}(\theta),AO=sen(\theta+d\theta)\approx sen(\theta) \right )

 \therefore  

 y_{P}=sen^{3}(\theta)

Temos que as coordenadas do ponto P são:

 (x,y)=(cos^{3}(\theta),sen^{3}(\theta))

Da trigonometria:  sen^{2}(\theta)+cos^{2}(\theta)=1

Então, a equação do lugar geométrico do ponto P será

 \boxed {x^{\frac{2}{3}}+y^{\frac{2}{3}}=1}  

O comportamento do ponto P, descrito pela equação acima, pode ser entendido ao observar a imagem abaixo.


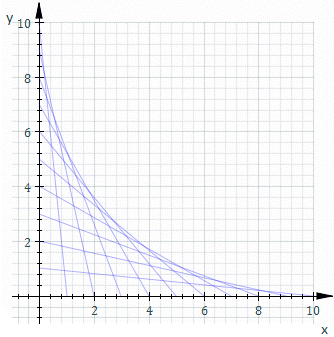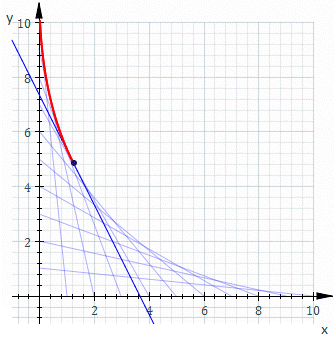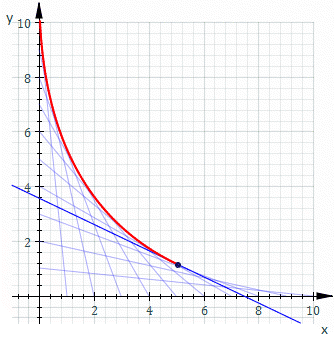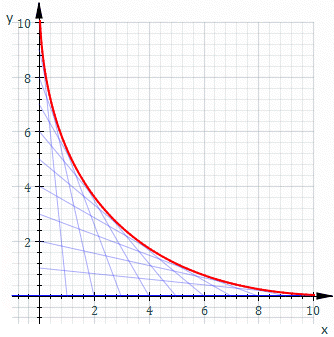
Não dê bola aos valores deste gráfico 

Espero que seja isso.

Numa construção "régua e compasso", no Geogebra:

Bonito trabalho, Gilberto!
Em qual programa você fez esse gráfico animado?

Medeiros escreveu:Bonito trabalho, Gilberto!
Em qual programa você fez esse gráfico animado?

Tirei da wikipedia. Aliás, falha minha não ter mencionado isso. 

https://en.wikipedia.org/wiki/Envelope_(mathematics)

Outra solução... 



 DO = cos(\theta)
CO = sen(\theta)
DB = sen(\theta)d\theta
CA = cos(\theta)d\theta

Pelo teorema de Menelaus:

 \frac{PA}{PB}.\frac{DB}{DO}.\frac{CO}{CA}=1

 \frac{PA}{PB}.\frac{sen(\theta)d\theta}{cos(\theta)}.\frac{sen(\theta)}{cos(\theta)d\theta}=1

 \frac{PA}{PB}=k=\frac{cos^{2}(\theta)}{sen^{2}(\theta)}

 \frac{PA}{1-PA}=k

 PA=\frac{k}{1+k}=cos^{2}(\theta)

 \Delta AGP\sim \Delta AOB

 \therefore  

 \frac{x}{OB}=\frac{AP}{1}\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, (\because PG=x,AB=1)

 x=cos^{3}(\theta)\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, (\because OB=cos(\theta+d\theta)\approx cos(\theta))

No triângulo AGP:

 AG=x.tan(\theta+d\theta)=cos^{3}(\theta)tan(\theta)=sen(\theta)cos^{2}(\theta)

 y=AO-AG=sen(\theta+d\theta)-sen(\theta)cos^{2}(\theta)\approx sen(\theta)(1-cos^{2}(\theta))

y = sen^{3}(\theta)

 \therefore  

 (x,y)=(cos^{3}(\theta),sen^{3}(\theta))\Rightarrow x^{\frac{2}{3}}+y^{\frac{2}{3}}=1  

Mesmo resultado.

essa segunda solução você acrescentou depois de me dar a resposta; depois a vejo com calma.

De qualquer forma, entendo que, por terem mesmo resultado, ambas as soluções não atendem ao exercício pois, conforme o Élcioschin calculou e eu desenhei, o trajeto do ponto médio da escada é uma circunferência. Se desenharmos a escada a 45º vemos que seu ponto médio fica fora das curvas apresentadas nas respostas.

Noto que o gráfico do Euclides fornece a posição correta.

Gente, meu Deus, perdão! Eu que errei no enunciado, porque meu professor falou isso (envelope) e eu entendi errado :/ Achava que eram os pontos de tangência.

Muá escreveu:Gente, meu Deus, perdão! Eu que errei no enunciado, porque meu professor falou isso (envelope) e eu entendi errado :/ Achava que eram os pontos de tangência.

Tinha quase certeza... Já vi esse enunciado há alguns anos (2014), mas não tinha conseguido resolver.