Integral de Linha
2 participantes
Página 1 de 1
 Integral de Linha
Integral de Linha
Olá pessoal,tudo bem ?
estou em dúvida em relação a esta questão:
Calcular a integral (2x -y + z), onde C é o segmento de reta que liga os pontos
A(1,2,3) a B(2,0,1) . (resposta: 12)
Tentei fazer assim:
A(1,2,3)
B-A= (1,-2,-2)
X(T) = 1+T
Y(T) = 2-2T
Z(T) = 3-2T
a integral ficaria :
integral de : (2* (1+T) -(2-2t) + (3-2t)
porém o valor não está dando 12.Aonde está o erro ?
estou em dúvida em relação a esta questão:
Calcular a integral (2x -y + z), onde C é o segmento de reta que liga os pontos
A(1,2,3) a B(2,0,1) . (resposta: 12)
Tentei fazer assim:
A(1,2,3)
B-A= (1,-2,-2)
X(T) = 1+T
Y(T) = 2-2T
Z(T) = 3-2T
a integral ficaria :
integral de : (2* (1+T) -(2-2t) + (3-2t)
porém o valor não está dando 12.Aonde está o erro ?

saidmrn- Iniciante
- Mensagens : 3
Data de inscrição : 18/09/2011
Idade : 28
Localização : Brasil-Para-Belem
 Re: Integral de Linha
Re: Integral de Linha
O seu vetor AB está correto.

Como o ponto B = (2,0,0), temos que a forma parametrizada pode ser escrita como:

Lembre-se que o intervalo de t para a parametrização de uma reta é dado por:
Consegue concluir sozinho?
Como o ponto B = (2,0,0), temos que a forma parametrizada pode ser escrita como:
Lembre-se que o intervalo de t para a parametrização de uma reta é dado por:
Consegue concluir sozinho?

Mathimatiká Grecca- Jedi

- Mensagens : 200
Data de inscrição : 26/08/2015
Idade : 32
Localização : São Paulo - SP
 Re: Integral de Linha
Re: Integral de Linha
olá,não devia multiplicar o vetor AB pelo ponto A,em vez do ponto B ?Mathimatiká Grecca escreveu:O seu vetor AB está correto.
Como o ponto B = (2,0,1), temos que a forma parametrizada pode ser escrita como:
Lembre-se que o intervalo de t para a parametrização de uma reta é dado por:
Consegue concluir sozinho?
Tentei integrar também com os seus valores e também não deu 12,devo estar fazendo algo errado.
Me desculpe pelo trabalho.Obrigado !

saidmrn- Iniciante
- Mensagens : 3
Data de inscrição : 18/09/2011
Idade : 28
Localização : Brasil-Para-Belem
 Re: Integral de Linha
Re: Integral de Linha
Olá!
1° Passo: Encontrar uma parametrização lisa de C.
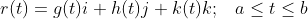
2° Passo: Calcular a integral como:
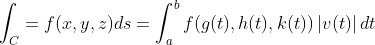
Como encontramos que
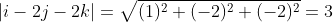
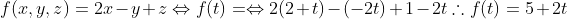
Agora basta resolver a integral:
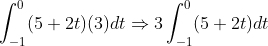
Resolvendo-a, temos:
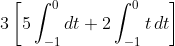
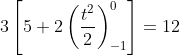
Agora ficou mais claro?
1° Passo: Encontrar uma parametrização lisa de C.
2° Passo: Calcular a integral como:
Como encontramos que
Agora basta resolver a integral:
Resolvendo-a, temos:
Agora ficou mais claro?

Mathimatiká Grecca- Jedi

- Mensagens : 200
Data de inscrição : 26/08/2015
Idade : 32
Localização : São Paulo - SP
 Re: Integral de Linha
Re: Integral de Linha
Muito Obrigado,você é a melhor,resolução perfeita e tirou muitas dúvidas de outras questões !
Obrigado !
Obrigado !

saidmrn- Iniciante
- Mensagens : 3
Data de inscrição : 18/09/2011
Idade : 28
Localização : Brasil-Para-Belem
 Re: Integral de Linha
Re: Integral de Linha
Que bom que você entendeu. 
Obrigada
Obrigada

Mathimatiká Grecca- Jedi

- Mensagens : 200
Data de inscrição : 26/08/2015
Idade : 32
Localização : São Paulo - SP
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












