Funções circulares (FME)
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Funções circulares (FME)
por Ada Augusta Sáb 27 Abr 2024, 13:35
126. Represente, no ciclo, as imagens dos seguintes conjuntos de números reais:
Gab.:
Não entendi F nem G. Em F não deveria ser representado nos pontos π/2, π, 3π/2 e 2π e seus derivados?
Em G, não entendi por que P2 e P4 não entraram na imagem.
Gab.:
Não entendi F nem G. Em F não deveria ser representado nos pontos π/2, π, 3π/2 e 2π e seus derivados?
Em G, não entendi por que P2 e P4 não entraram na imagem.
Ada Augusta- Jedi
- Mensagens : 228
Data de inscrição : 08/09/2023
Re: Funções circulares (FME)
por Leonardo Mariano Sáb 27 Abr 2024, 18:08
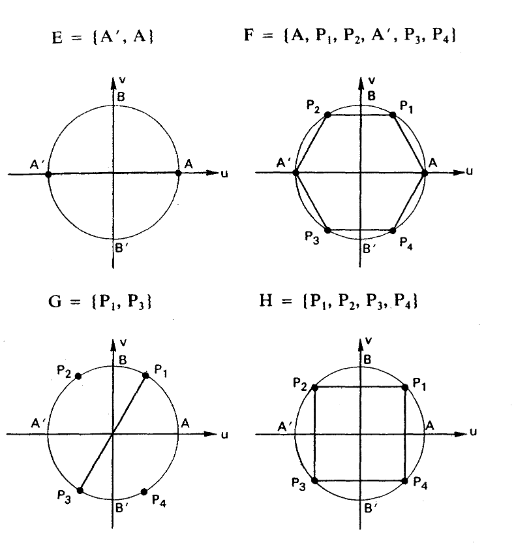
Boa tarde Ada, creio que haja uma incoerência no enunciado que você possui, pelo menos pesquisando aqui no FME eu encontrei esta questão desta forma:
Ou seja, em F na verdade o denominador é 3, por isso gerou a incoerência.
Já em G:
[latex] k = 0: x = \frac{\pi}{3} + 0\pi
k = 1: x = \frac{\pi}{3} + \pi =\frac{4\pi}{3} [/latex]
Os únicos ponto são estes acima, π/3 e 4π/3, a partir de k = 2 as soluções apenas se repetem.
Ou seja, em F na verdade o denominador é 3, por isso gerou a incoerência.
Já em G:
[latex] k = 0: x = \frac{\pi}{3} + 0\pi
k = 1: x = \frac{\pi}{3} + \pi =\frac{4\pi}{3} [/latex]
Os únicos ponto são estes acima, π/3 e 4π/3, a partir de k = 2 as soluções apenas se repetem.
Leonardo Mariano- Monitor
- Mensagens : 643
Data de inscrição : 11/11/2018
Idade : 22
Localização : Criciúma/SC
Ada Augusta gosta desta mensagem
Re: Funções circulares (FME)
por Ada Augusta Sáb 27 Abr 2024, 19:01
Nossa, fiquei empolgada de ter conseguido o solucionário do FME e nem me toquei que poderia ser de versões diferentes. Sobre a G, tinha utilizado o mesmo caso da F, mas com a sua solução percebi meu erro. Obrigada!!
Ada Augusta- Jedi
- Mensagens : 228
Data de inscrição : 08/09/2023
Leonardo Mariano gosta desta mensagem
Tópicos semelhantes» Funções circulares
» funcoes circulares
» Funçoes circulares
» Funções circulares
» FUNÇÕES CIRCULARES
» funcoes circulares
» Funçoes circulares
» Funções circulares
» FUNÇÕES CIRCULARES
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
