Integral de linha

por **alansilva** Qui 02 Mar 2017, 15:57

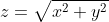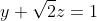Uma curva C tem a forma da interseção da superfícies $Integral de linha Gif$ e $Integral de linha Gif$ . Calcule a integral de linha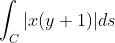 $Integral de linha Gif$

por **mauk03** Sáb 04 Mar 2017, 02:26

$\left\{\begin{matrix} z=\sqrt{x^2+y^2}\\ y+\sqrt{2}z=1 \end{matrix}\right.\Rightarrow \sqrt{2}\sqrt{x^2+y^2}=1-y\Rightarrow 2(x^2+y^2)=1-2y+y^2$ $\Rightarrow x^2+\frac{(y+1)^2}{2}=1$

A intersecção trata-se de uma elipse que pode ter a seguinte parametrização:
$(x,y)=(\cos t,\sqrt{2}\sin t-1)$ , com $0\leq t\leq 2\pi$

$z=\frac{1-y}{\sqrt{2}}=\frac{1-\sqrt{2}\sin t+1}{\sqrt{2}}=\sqrt{2}-\sin t$

$ds=\sqrt{\left ( \frac{dx}{dt} \right )^2+\left ( \frac{dy}{dt} \right )^2+\left ( \frac{dz}{dt} \right )^2}dt=\sqrt{\left ( -\sin t \right )^2+\left ( \sqrt{2}\cos t \right )^2+\left ( -\cos t \right )^2}dt$
$=\sqrt{\sin^2 t+3\cos^2 t}dt=\sqrt{1+2\cos^2 t}dt$

Assim:
$\int _{C}|x(y+1)|ds=\int_{0}^{2\pi}|\cos t(\sqrt{2}\sin t-1+1)|\sqrt{1+2\cos^2 t}dt=\sqrt{2}\int_{0}^{2\pi}|\cos t\sin t|\sqrt{1+2\cos^2 t}dt$

Pra resolver essa integral basta desmembrá-la em outras integrais com diferentes intervalos dentro de [0, 2pi] de acordo com o sinal do produto cos(t)sin(t) (de modo a eliminar o modulo da expressão) e para resolver essas integrais fazer a mudança de variavel u=cos(t).

por **alansilva** Sáb 04 Mar 2017, 10:09

Eu estou achando zero .
É igual ao seu resultado???

por **alansilva** Sáb 04 Mar 2017, 10:12

mauk03 escreveu: $\left\{\begin{matrix} z=\sqrt{x^2+y^2}\\ y+\sqrt{2}z=1 \end{matrix}\right.\Rightarrow \sqrt{2}\sqrt{x^2+y^2}=1-y\Rightarrow 2(x^2+y^2)=1-2y+y^2$ $\Rightarrow x^2+\frac{(y+1)^2}{2}=1$

A intersecção trata-se de uma elipse que pode ter a seguinte parametrização:
$(x,y)=(\cos t,\sqrt{2}\sin t-1)$ , com $0\leq t\leq 2\pi$

$ds=\sqrt{\left ( \frac{dx}{dt} \right )^2+\left ( \frac{dy}{dt} \right )^2}dt=\sqrt{\left ( -\sin t \right )^2+\left ( \sqrt{2}\cos t \right )^2}dt$
$=\sqrt{\sin^2 t+2\cos^2 t}dt=\sqrt{1+\cos^2 t}dt$

Assim:
$\int _{C}|x(y+1)|ds=\int_{0}^{2\pi}|\cos t(\sqrt{2}\sin t-1+1)|\sqrt{1+\cos^2 t}dt=\sqrt{2}\int_{0}^{2\pi}|\cos t\sin t|\sqrt{1+\cos^2 t}dt$

Pra resolver essa integral basta desmembrá-la em outras integrais com diferentes intervalos dentro de [0, 2pi] de acordo com o sinal do produto cos(t)sin(t) (de modo a eliminar o modulo da expressão) e para resolver essas integrais fazer a mudança de variavel u=cos(t).

Só não entendi pq não achou o valor de z.

por **mauk03** Sáb 04 Mar 2017, 13:09

alansilva escreveu:
mauk03 escreveu: $\left\{\begin{matrix} z=\sqrt{x^2+y^2}\\ y+\sqrt{2}z=1 \end{matrix}\right.\Rightarrow \sqrt{2}\sqrt{x^2+y^2}=1-y\Rightarrow 2(x^2+y^2)=1-2y+y^2$ $\Rightarrow x^2+\frac{(y+1)^2}{2}=1$

A intersecção trata-se de uma elipse que pode ter a seguinte parametrização:
$(x,y)=(\cos t,\sqrt{2}\sin t-1)$ , com $0\leq t\leq 2\pi$

$ds=\sqrt{\left ( \frac{dx}{dt} \right )^2+\left ( \frac{dy}{dt} \right )^2}dt=\sqrt{\left ( -\sin t \right )^2+\left ( \sqrt{2}\cos t \right )^2}dt$
$=\sqrt{\sin^2 t+2\cos^2 t}dt=\sqrt{1+\cos^2 t}dt$

Assim:
$\int _{C}|x(y+1)|ds=\int_{0}^{2\pi}|\cos t(\sqrt{2}\sin t-1+1)|\sqrt{1+\cos^2 t}dt=\sqrt{2}\int_{0}^{2\pi}|\cos t\sin t|\sqrt{1+\cos^2 t}dt$

Pra resolver essa integral basta desmembrá-la em outras integrais com diferentes intervalos dentro de [0, 2pi] de acordo com o sinal do produto cos(t)sin(t) (de modo a eliminar o modulo da expressão) e para resolver essas integrais fazer a mudança de variavel u=cos(t).

Só não entendi pq não achou o valor de z.

Tem razão esqueci do z, vou editar.

por **mauk03** Sáb 04 Mar 2017, 13:18

alansilva escreveu:Eu estou achando zero .
É igual ao seu resultado???

apenas se desconsiderar o modulo, com o modulo fica igual a:
http://www.wolframalpha.com/input/?i=int+sqrt(2)abs(cos(x)sin(x))sqrt(1%2B2cos%5E2(x))dx+from+x%3D0+to+2pi

por Conteúdo patrocinado

Integral de linha

Integral de linha

Re: Integral de linha

Re: Integral de linha

Re: Integral de linha

Re: Integral de linha

Re: Integral de linha

Re: Integral de linha

Um fórum livre e democrático.