inequações trigonométricas

por lucaseasy Sex 04 Set 2015, 03:01

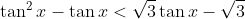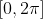a questão pede para resolver $inequações trigonométricas Gif$ , no intervalo $inequações trigonométricas Gif$ :

resolvendo...
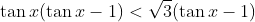
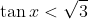
$inequações trigonométricas Gif$

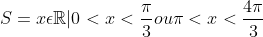
$inequações trigonométricas Gif$

minha resposta

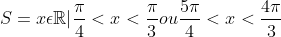
$inequações trigonométricas Gif$

só que a resposta não é essa, e sim essa : $inequações trigonométricas Gif$

grato desde já!

por **Elcioschin** Sex 04 Set 2015, 03:42

tg²x - tgx - √3.tgx + √3 < 0 ---> tg²x - (1 + √3).x + √3 < 0 ---> Função do 2º grau na variável tgx

∆ = b² - 4.ac ---> ∆ = (1 + √3)² - 4.1.√3 ---> ∆ = 1² - 2.√3 + (√3)² - 4.√3 ---> ∆ = 1² - 2.√3 + (√3)² --->

∆ = (1 - √3)² ---> √∆ = 1 - √3

Raízes --->

tgx = [(1 + √3) + (1 - √3)]/2 ---> tgx = 1 ---> x = pi/4 ou x = 5.pi/4

tgx = [(1 + √3) - (1 - √3)]/2 ---> tgx = √3 ---> x = pi/3 ou x = 4.pi/3

Desenhe um círculo trigonométrico, plote os ângulos e confira.
O gabarito está certo

inequações trigonométricas

inequações trigonométricas

Re: inequações trigonométricas

Um fórum livre e democrático.