Teoria dos Números
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Teoria dos Números
Teoria dos Números
Prove que todo número par maior que 3 pode ser escrito como a soma de dois números primos!
Estou há um bom tempo tentando resolver esse problema que um professor me passou, entretanto, ainda não consegui alcançar uma resposta, por mais que tenha chegado a algumas conclusões!
Poderiam me ajudar? Agradeço desde já qualquer posterior resposta!
Estou há um bom tempo tentando resolver esse problema que um professor me passou, entretanto, ainda não consegui alcançar uma resposta, por mais que tenha chegado a algumas conclusões!
Poderiam me ajudar? Agradeço desde já qualquer posterior resposta!

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Re: Teoria dos Números
Re: Teoria dos Números
Disposição do regulamento do fórum:
XII- O fórum está dividido em seções específicas. Poste sua questão na seção adequada ao assunto. Questões fora de lugar poderão ser bloqueadas ou apagadas pelos moderadores.
Esta é a seção de Físico-Química. Sua dúvida é relativa a outra seção.
XII- O fórum está dividido em seções específicas. Poste sua questão na seção adequada ao assunto. Questões fora de lugar poderão ser bloqueadas ou apagadas pelos moderadores.
Esta é a seção de Físico-Química. Sua dúvida é relativa a outra seção.
 Re: Teoria dos Números
Re: Teoria dos Números
Desculpe, não percebi isso! Como altero?

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Re: Teoria dos Números
Re: Teoria dos Números
Movido para Algebra.
Sendo dois primos, p e q, temos que eles não serão multiplos de 2.
E portanto, podemos escrever eles de maneira:
p = 2m + 1
q = 2n + 1
Donde m e n são naturais.
Assim, se temos a soma dos dois primos, podemos reescrever:
p + q = (2m+1)+(2n+1) = 2m+2n+2 = 2(m+n+1)
Como m, n e 1 são inteiros, temos então um multiplo de 2.
Existem outras formas de provar. Dê uma pesquisada em Conjectura de Goldbach, que diz que qualquer número natural (maior que 6) pode ser escrito como a soma de 3 números primos. Ainda é chamada de teoria pois ainda não foi provada.
6 = 2 + 2 +2
7 = 2 + 3 + 2
8 = 3 + 3 + 2
9 = 3 + 3 + 3
10 = 5 + 3 + 2
11 = 7 + 2 + 2 = 5 + 3 + 3
...
Christian Goldbach em sua troca de cartas com Euler, propôs que Euler provasse. E como sabemos que até hoje não foi provada, pode-se concluir que Euler não teve êxito no "desafio". Mas Euler propôs outra:
Qualquer número natural maior que 4 pode ser escrito como a soma de dois primos:
4 = 2 + 2
5 = 3 + 2
6 = 3 + 3
7 = 5 + 2
8 = 5 + 3
9 = 7 + 2
10 = 7 + 3
...
Na época eles consideravam 1 como primo, então acho que era maior que 3 na conjectura de goldbach e maior que 2 que Euler propôs. Mas para evitar confusões se 1 é primo ou não, coloquei acima de 6 e 4.
Mais detalhes em:
Wikipédia - Conjetura de Goldbach
Não sou matemático e nem conheço bem pra dizer se concordo, mas pelo pouco que sei, o que está escrito lá está correto - Wikipédia nem sempre é confiável.
Sendo dois primos, p e q, temos que eles não serão multiplos de 2.
E portanto, podemos escrever eles de maneira:
p = 2m + 1
q = 2n + 1
Donde m e n são naturais.
Assim, se temos a soma dos dois primos, podemos reescrever:
p + q = (2m+1)+(2n+1) = 2m+2n+2 = 2(m+n+1)
Como m, n e 1 são inteiros, temos então um multiplo de 2.
Existem outras formas de provar. Dê uma pesquisada em Conjectura de Goldbach, que diz que qualquer número natural (maior que 6) pode ser escrito como a soma de 3 números primos. Ainda é chamada de teoria pois ainda não foi provada.
6 = 2 + 2 +2
7 = 2 + 3 + 2
8 = 3 + 3 + 2
9 = 3 + 3 + 3
10 = 5 + 3 + 2
11 = 7 + 2 + 2 = 5 + 3 + 3
...
Christian Goldbach em sua troca de cartas com Euler, propôs que Euler provasse. E como sabemos que até hoje não foi provada, pode-se concluir que Euler não teve êxito no "desafio". Mas Euler propôs outra:
Qualquer número natural maior que 4 pode ser escrito como a soma de dois primos:
4 = 2 + 2
5 = 3 + 2
6 = 3 + 3
7 = 5 + 2
8 = 5 + 3
9 = 7 + 2
10 = 7 + 3
...
Na época eles consideravam 1 como primo, então acho que era maior que 3 na conjectura de goldbach e maior que 2 que Euler propôs. Mas para evitar confusões se 1 é primo ou não, coloquei acima de 6 e 4.
Mais detalhes em:
Wikipédia - Conjetura de Goldbach
Não sou matemático e nem conheço bem pra dizer se concordo, mas pelo pouco que sei, o que está escrito lá está correto - Wikipédia nem sempre é confiável.
____________________________________________
← → ↛  ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥
 ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
 ℛ ℜ ℰ ℳ ℊ ℒ
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor

- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
 Re: Teoria dos Números
Re: Teoria dos Números
Bem, então podemos especificar mais ainda, e dizer que todos números pares maior que 4 podem ser escritos como a soma de dois números primos diferentes de 2?
Uma vez que o número 2 é primo, e reescrevemos o número p (primo), como 2m + 1, o que excluiria a possibilidade do número p ser o próprio 2!!
E quanto a "Qualquer número natural maior que 4 pode ser escrito como a soma de dois primos":
4 = 2 + 2
5 = 3 + 2
6 = 3 + 3
7 = 5 + 2
8 = 5 + 3
9 = 7 + 2
10 = 7 + 3
Teríamos como próximo número dessa sequência o 11, que não pode ser escrito como a soma de 2 números primos, o que invalidaria o teorema!
Uma vez que o número 2 é primo, e reescrevemos o número p (primo), como 2m + 1, o que excluiria a possibilidade do número p ser o próprio 2!!
E quanto a "Qualquer número natural maior que 4 pode ser escrito como a soma de dois primos":
4 = 2 + 2
5 = 3 + 2
6 = 3 + 3
7 = 5 + 2
8 = 5 + 3
9 = 7 + 2
10 = 7 + 3
Teríamos como próximo número dessa sequência o 11, que não pode ser escrito como a soma de 2 números primos, o que invalidaria o teorema!

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Re: Teoria dos Números
Re: Teoria dos Números
Correção:
Mostrei pra dois impares qualquer.
Mas é nessário que sejam primos, nada nos garante que p e q são primos.
Dei uma procurada, e então, o que consegui for por congruência:
Sendo p um primo qualquer, temos que pelo pequeno teorema de Fermat, que nos diz:
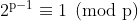
Desde que mdc(2, p) = 1
Logo, podemos escrever
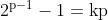
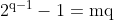
Assim, a soma de p e q:
}{km}})
Como 2^(p-1) e 2^(q-1) são multiplos de 2, então espera-se que m . 2^(p-1) + k . p^(q-1) sejam multiplos de 2.
Como 2^(p-1) - 1 = kp e 2^(q-1) - 1 = mq, então podemos concluir que k e m são impares, o que faz com que sua soma seja par.
Ou seja, todo o numerador é par. Agora, para mostrar que a soma de dois primos resulta em um número par, basta que o numerador seja multiplo do denominador. Para isso:
&space;\equiv&space;k&space;\cdot&space;2^{q-1}&space;-&space;k&space;\pmod{m}}&space;\\&space;\mathrm{&space;k&space;\left(2^{q-1}-1&space;\right&space;)&space;\equiv&space;k&space;\cdot&space;mq&space;\equiv&space;0&space;\pmod{&space;m}})
Logo, o numerador é multiplo de m.
Agora, de modo análogo para k:
&space;\equiv&space;m&space;\cdot&space;2^{p-1}&space;-&space;m&space;\pmod{k}}&space;\\&space;\mathrm{&space;m&space;\left(2^{p-1}-1&space;\right&space;)&space;\equiv&space;m&space;\cdot&space;kp&space;\equiv&space;0&space;\pmod{&space;k}})
Logo, se o numerador é multiplo de 2, de k, de m, então significa que p+q é inteiro e multiplo de 2.
Ou seja, para que p+q seja multiplo de 2, basta que mdc(2, p) = mdc(2, q) = 1, independendo se são primos ou não.
Agora acho que foi uma resposta melhor.
Agora respondendo à sua pergunta:
Interpretei errado e coloquei a conjectura de Goldbach para Euler também, o que não é o caso.
"Euler, se interessando pelo problema, respondeu que a conjetura era equivalente à outra:
Todo inteiro par maior que 2 pode ser escrito como a soma de 2 números primos.
— Euler respondendo a Goldbach"
E você está correto: partir de um momento, não podemos escrever impares como soma de 2 primos, isso porque teriamos que utilizar sempre 2 na soma com outro primo para obter outro primo. O que não ocorre.
Há primos que dão certo porque são "vizinhos", por exemplo 11 e 13, 17 e 19, 29 e 31, 41 e 43, ...
O que Euler respondeu é que a soma de qualquer par era a soma de dois primos.
Mostrei pra dois impares qualquer.
Mas é nessário que sejam primos, nada nos garante que p e q são primos.
Dei uma procurada, e então, o que consegui for por congruência:
Sendo p um primo qualquer, temos que pelo pequeno teorema de Fermat, que nos diz:
Desde que mdc(2, p) = 1
Logo, podemos escrever
Assim, a soma de p e q:
Como 2^(p-1) e 2^(q-1) são multiplos de 2, então espera-se que m . 2^(p-1) + k . p^(q-1) sejam multiplos de 2.
Como 2^(p-1) - 1 = kp e 2^(q-1) - 1 = mq, então podemos concluir que k e m são impares, o que faz com que sua soma seja par.
Ou seja, todo o numerador é par. Agora, para mostrar que a soma de dois primos resulta em um número par, basta que o numerador seja multiplo do denominador. Para isso:
Logo, o numerador é multiplo de m.
Agora, de modo análogo para k:
Logo, se o numerador é multiplo de 2, de k, de m, então significa que p+q é inteiro e multiplo de 2.
Ou seja, para que p+q seja multiplo de 2, basta que mdc(2, p) = mdc(2, q) = 1, independendo se são primos ou não.
Agora acho que foi uma resposta melhor.
Agora respondendo à sua pergunta:
Interpretei errado e coloquei a conjectura de Goldbach para Euler também, o que não é o caso.
"Euler, se interessando pelo problema, respondeu que a conjetura era equivalente à outra:
Todo inteiro par maior que 2 pode ser escrito como a soma de 2 números primos.
— Euler respondendo a Goldbach"
E você está correto: partir de um momento, não podemos escrever impares como soma de 2 primos, isso porque teriamos que utilizar sempre 2 na soma com outro primo para obter outro primo. O que não ocorre.
Há primos que dão certo porque são "vizinhos", por exemplo 11 e 13, 17 e 19, 29 e 31, 41 e 43, ...
O que Euler respondeu é que a soma de qualquer par era a soma de dois primos.
____________________________________________
← → ↛  ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥
 ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
 ℛ ℜ ℰ ℳ ℊ ℒ
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor

- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
 Re: Teoria dos Números
Re: Teoria dos Números
Agora eu entendi!! Obrigado pela ajuda!

Matemathiago- Estrela Dourada

- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Teoria dos números
» [Teoria dos números] Números perfeitos
» Teoria dos números
» Teoria dos números
» Teoria dos números
» [Teoria dos números] Números perfeitos
» Teoria dos números
» Teoria dos números
» Teoria dos números
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













