(EFOMM - 2016) Geometria
2 participantes
Página 1 de 1
(EFOMM - 2016) Geometria
por RamonLucas Seg 03 Ago 2015, 12:39
PROVA: BRANCA FIS - MAT 2016-1. 9° Questão.
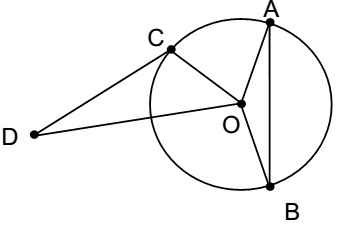
Determine o comprimento do menor arco AB na circunferência de centro O, representada na figura a seguir, sabendo que o segmento OD mede 12cm, os ângulos CÔD = 30° e OÂB = 15° e que a área do triângulo CDO é igual a 18 cm2.
( a ) 5∏ cm
( b ) 12 cm
( c ) 5 cm
( d ) 12∏ cm
( e ) 10∏ cm
Determine o comprimento do menor arco AB na circunferência de centro O, representada na figura a seguir, sabendo que o segmento OD mede 12cm, os ângulos CÔD = 30° e OÂB = 15° e que a área do triângulo CDO é igual a 18 cm2.
( a ) 5∏ cm
( b ) 12 cm
( c ) 5 cm
( d ) 12∏ cm
( e ) 10∏ cm
RamonLucas- Estrela Dourada
- Mensagens : 2034
Data de inscrição : 26/03/2015
Idade : 31
Localização : Brasil, Búzios.
Re: (EFOMM - 2016) Geometria
por Hoshyminiag Seg 03 Ago 2015, 14:34
A área de um triângulo pode ser dada pelo semi produto de dois lados vezes o seno do ângulo formado entre eles.
Área do triângulo CDO = sen 30 . (OD . OC)/2 = 18
Sendo OD = 12 e OC = r, temos:
(1/2) . (12.r)/2 = 18 <--> r = 6
O triângulo BOA é isósceles, logo AÔB = 150º. Portanto, o arco AB mede 150º
O comprimento de uma circunferência (360º) é 2∏.r
Regra de 3
360º ------- 2∏.r
150º ------- x
x = 2∏.r . 5/12 = 2∏.6 . 5/12 = 5∏
(A)
Área do triângulo CDO = sen 30 . (OD . OC)/2 = 18
Sendo OD = 12 e OC = r, temos:
(1/2) . (12.r)/2 = 18 <--> r = 6
O triângulo BOA é isósceles, logo AÔB = 150º. Portanto, o arco AB mede 150º
O comprimento de uma circunferência (360º) é 2∏.r
Regra de 3
360º ------- 2∏.r
150º ------- x
x = 2∏.r . 5/12 = 2∏.6 . 5/12 = 5∏
(A)
Hoshyminiag- Mestre Jedi
- Mensagens : 705
Data de inscrição : 06/07/2014
Idade : 24
Localização : Rio de Janeiro; Rio de Janeiro; Brasil
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
