Geometria analitica - AFA

por jaques104 Sáb 25 Abr 2015, 19:42

Relembrando a primeira mensagem :

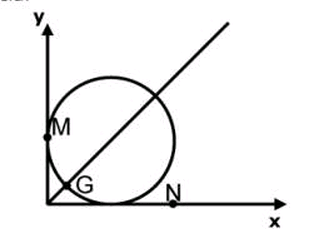
A circunferência (λ) x² + y² – 2x – 2y + k = 0 passa pelo ponto
A(0, 1). Sabendo-se que o ponto P de (λ) mais próximo da
origem coincide com o baricentro do triângulo MNQ, onde
M(0, k), N(2k, 0) e Q(xQ, yQ) é correto afirmar que a área do
triângulo MNQ é um número do intervalo

Geometria analitica - AFA - Página 2 603f1adef04af469c035fc5a39d363dd

Geometria analitica - AFA - Página 2 603f1adef04af469c035fc5a39d363dd

por jaques104 Sáb 25 Abr 2015, 22:03

Medeiros escreveu:
jaques104 escreveu:
eu não entendi pq P é o encontro da reta x = y, desenhando o gráfico parece bem intuitivo, porém apenas isso basta, não tem nenhuma propriedade por detrás?
Não há nada de "intuitivo" nisto, você está vendo a construção, a coisa real, não apenas números ou letras numa fileira algébrica.

Porém, se quisermos dar foros de cálculo aritmético a esta evidência, podemos fazer:
1) a menor distância entre uma circunferência e um ponto externo a ela está sobre uma reta que passa por seu centro.
λ -----> r=1, C (1,1)
origem ----> O (0,0)
Logo, P pertence à reta y=x (bissetriz dos quadrantes ímpares).

2) d (O, C) = √2
descontando o raio ----> d (O, P) = √2 - 1
donde, xP.√2 = √2 - 1 -------> xP = yP = 1 - √2/2

ADENDO: Ashitaka, vejo, agora, que você deu esta mesma explicação faz 20min. Sinto ter repetido, de qualquer forma já escrevi, vou deixar.

entendi agora Medeiros

por **Ashitaka** Sáb 25 Abr 2015, 22:09

Que bom que entendeu. Agora deveria se lembrar de agradecer aos que te ajudam, em qualquer lugar. É um costume saudável para se manter e que, infelizmente, as pessoas estão perdendo.

por jaques104 Dom 26 Abr 2015, 10:15

Muito obrigado a todos!

por Lucas_DN684 Sáb 12 Ago 2023, 05:06

jaques104 escreveu:
Ashitaka escreveu:
Esse ponto P é o de encontro da reta y = x com a circunferência:
2(x-1)² = 1
x-1 = -1/√2
x = -1/√2 + 1
P(-1/√2 + 1, -1/√2 + 1)

-1/√2 + 1 = (0 + 2 + xQ)/3
-3/√2 + 1 = xQ
Analogamente, yQ = (-3/√2 + 1)

eu não entendi pq P é o encontro da reta x = y, desenhando o gráfico parece bem intuitivo, porém apenas isso não basta, não tem nenhuma propriedade por detrás?

"Teorema. A menor distância de um ponto fora de um círculo até um ponto no círculo é igual à distância do ponto ao centro do círculo menos o raio do círculo.

Prova à maneira de Euclides. Seja A o centro do círculo e B o ponto fora do círculo. Conecte os pontos A e B com uma linha reta [segmento] AB. Seja C o ponto de interseção do círculo com AB. Então AC + CB = AB. Seja D qualquer outro ponto no círculo. Pela desigualdade triangular, Euclides I.20, AB < AD + BD. Portanto, AC + CB < AD + BD. Mas AC e AD são iguais, sendo raios do círculo. Logo, CB < BD. Assim, C é o ponto mais próximo no círculo de B. E a distância de C a B é igual à distância de B a A menos o raio do círculo. Q.E.D.

Note que quando Euclides usava o termo "linha", ele se referia ao que entendemos por segmento de reta." (Joyce, 2015)¹

1: Joyce, David. “How Can I Prove Mathematically That the Smallest Distance from the Origin to the Circle Shown Is the Distance from the Origin to the Centre, Minus the Radius?” Quora, 2015, www.quora.com/How-can-I-prove-mathematically-that-the-smallest-distance-from-the-origin-to-the-circle-shown-is-the-distance-from-the-origin-to-the-centre-minus-the-radius. Accessed 12 Aug. 2023.