Geometria analitica - AFA

por jaques104 Sáb 25 Abr 2015, 19:42

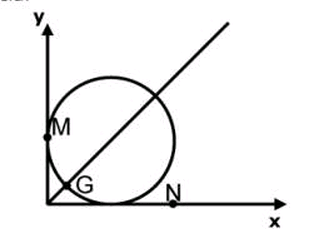
A circunferência (λ) x² + y² – 2x – 2y + k = 0 passa pelo ponto
A(0, 1). Sabendo-se que o ponto P de (λ) mais próximo da
origem coincide com o baricentro do triângulo MNQ, onde
M(0, k), N(2k, 0) e Q(xQ, yQ) é correto afirmar que a área do
triângulo MNQ é um número do intervalo

Geometria analitica - AFA 603f1adef04af469c035fc5a39d363dd

Geometria analitica - AFA 603f1adef04af469c035fc5a39d363dd

por **Ashitaka** Sáb 25 Abr 2015, 20:06

1 -2 + k = 0
k = 1

(x-1)² + (y-1)² = 1

Esse ponto P é o de encontro da reta y = x com a circunferência:
2(x-1)² = 1
x-1 = -1/√2
x = -1/√2 + 1
P(-1/√2 + 1, -1/√2 + 1)

-1/√2 + 1 = (0 + 2 + xQ)/3
-3/√2 + 1 = xQ

-1/√2 + 1 = (1 + 0 + yQ)/3
2 -3/√2 = yQ

Agora faça o determinante com os pontos:
M(0, 1), N(2, 0), Q(1-3/√2, 2-3/√2).
Pelo determinante, a área dá 9/√2 - 3 =~ 1,68, B.

por jaques104 Sáb 25 Abr 2015, 20:47

Ashitaka escreveu:
Esse ponto P é o de encontro da reta y = x com a circunferência:
2(x-1)² = 1
x-1 = -1/√2
x = -1/√2 + 1
P(-1/√2 + 1, -1/√2 + 1)

-1/√2 + 1 = (0 + 2 + xQ)/3
-3/√2 + 1 = xQ
Analogamente, yQ = (-3/√2 + 1)

eu não entendi pq P é o encontro da reta x = y, desenhando o gráfico parece bem intuitivo, porém apenas isso não basta, não tem nenhuma propriedade por detrás?
Geometria analitica - AFA 98a8e8b96bd0a41226213bd273754ddc

Geometria analitica - AFA 98a8e8b96bd0a41226213bd273754ddc

por **Ashitaka** Sáb 25 Abr 2015, 20:57

Pois é, é claro que ali é o ponto mais próximo, mas não sei como mostrar isso matematicamente através de equações. Note que para falar em distância, estamos falando da reta que une a orgem ao ponto P fazendo 90° com a circunferência; logo, tem que ser realmente ali, pois nenhum outro ponto ali faria 90°.
Eu até pensei em alguns modos de tentar demonstrar que ali é o ponto mais próximo, mas seriam bem trabalhosos e talvez até envolvessem derivadas. Talvez haja algum modo usando geometria plana ou uma álgebra mais fácil que não vi.

por **Medeiros** Sáb 25 Abr 2015, 21:02

Apenas dois detalhes:

1)
xP = yP = 1 - √2/2
mas enquanto xQ = 1 - 3√2/2, temos yQ = 2 - 3√2/2.

2)
Não é preciso obtermos as coordenadas de Q se já sabemos as do baricentro P.
área MNQ = 3×(área de MNP)
Lembrado que a área dada por três pontos é 1/2 do valor absoluto do determinante dos três pontos.
O cálculo por qualquer dos determinantes deverá resultar em A(MNQ)=~1,65 ----> alternativa B.

por **Ashitaka** Sáb 25 Abr 2015, 21:03

Não sei se é rigoroso o suficiente, mas poderia pensar que OC = √2. Assim, OP = √2 - R = √2 - 1, afinal a menor distância de O até C é uma reta (isso é um postulado), logo, para chegar de O até C, uma hora temos que tocar um ponto da circunferência. Ora, o primeiro ponto a ser tocado é o que está mais próximo de O, já que OC é mínimo. Portanto, OP = √2 - 1. Daí como a tangente de OC é 1, o ângulo entre OC e x é 45°.
x = OPcos45 = (√2 - 1)1/√2 = 1 - 1/√2
y = OPsen45 = (√2 - 1)1/√2 = 1 - 1/√2.

por **Ashitaka** Sáb 25 Abr 2015, 21:06

Medeiros escreveu:Apenas dois detalhes:

1)
xP = yP = 1 - √2/2
mas enquanto xQ = 1 - 3√2/2, temos yQ = 2 - 3√2/2.

2)
Não é preciso obtermos as coordenadas de Q se já sabemos as do baricentro P.
área MNQ = 3×(área de MNP)
Lembrado que a área dada por três pontos é 1/2 do valor absoluto do determinante dos três pontos.
O cálculo por qualquer dos determinantes deverá resultar em A(MNQ)=~1,65 ----> alternativa B.

1) Não entendi por que esse valor de yQ.

2) eu imaginei que haveria um modo de calcular sem achar o terceiro vértice, mas como não sou de confiar na minha geometria plana preferi fazer de uma vez.

por **Medeiros** Sáb 25 Abr 2015, 21:22

jaques104 escreveu:
eu não entendi pq P é o encontro da reta x = y, desenhando o gráfico parece bem intuitivo, porém apenas isso basta, não tem nenhuma propriedade por detrás?

Não há nada de "intuitivo" nisto, você está vendo a construção, a coisa real, não apenas números ou letras numa fileira algébrica.

Porém, se quisermos dar foros de cálculo aritmético a esta evidência, podemos fazer:
1) a menor distância entre uma circunferência e um ponto externo a ela está sobre uma reta que passa por seu centro.
λ -----> r=1, C (1,1)
origem ----> O (0,0)
Logo, P pertence à reta y=x (bissetriz dos quadrantes ímpares).

2) d (O, C) = √2
descontando o raio ----> d (O, P) = √2 - 1
donde, xP.√2 = √2 - 1 -------> xP = yP = 1 - √2/2

ADENDO: Ashitaka, vejo, agora, que você deu esta mesma explicação faz 20min. Sinto ter repetido, de qualquer forma já escrevi, vou deixar.

por **Medeiros** Sáb 25 Abr 2015, 21:37

Ashitaka,
os pontos M e N não são simétricos em relação à origem, eles têm coordenadas diferentes e, por isto, o cálculo da média resulta diferente para cada eixo.
(experimente, depois, realizar os cálculos pelos dois métodos)

Geometria analitica - AFA 1z3b9lv