Dúvida matemática
3 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Dúvida matemática
Dúvida matemática
Uma mesma equipe, com menos de 50 professores, corrigiu 3 edições de um exame, tendo sido possível dividir as provas igualitariamente entre eles nas duas primeiras, mas não na terceira. Da 1º para a 2º edição, o número de provas aumentou 185, mas da 2º para a 3º, houve uma redução de 140. Para uma 4º edição, o menor aumento nesse número, para que volte a ser possível distribuí-las por igual é:
01) 8
02) 15
03) 29
04) 37
05) 45
01) 8
02) 15
03) 29
04) 37
05) 45
Convidado- Convidado
 Re: Dúvida matemática
Re: Dúvida matemática
Seja p o número de professores e x o número de participantes na 1ª edição: x/p = k ---> x = p.k ---> k inteiro ---> k > 0
Número de participantes na 2ª edição = x + 185 ---> (x + 185)/p = m ---> m inteiro ---> m > 0
(p.k + 185)/p = m ---> k + 185/p = m ---> 185/p = m - k ---> 5.37/p = m - k
Temos duas possibilidades ---> p = 5 ou p = 37
1) Para p = 5 ---> m - k = 37 ---> x = 5.k
Participantes da 3ª edição ---> (x + 185 - 140)/p = (5.k + 45)/5 = k + 9 ---> inteiro ---> Não serve
2) Para p = 37 ---> m - k = 5 ---> x = 37.k ---> (37.k +45)/37 = m - k ---> k + 45/37 = m - k ---> m - 2k = 45/37
m - 2k = (45 + 29 - 29)/37 ---> m - 2k = (74 - 29)/37 ---> m - k = 2 - 29/37
Para a 4ª edição ser distribuída igualmente o menor aumento deverá ser 29
Número de participantes na 2ª edição = x + 185 ---> (x + 185)/p = m ---> m inteiro ---> m > 0
(p.k + 185)/p = m ---> k + 185/p = m ---> 185/p = m - k ---> 5.37/p = m - k
Temos duas possibilidades ---> p = 5 ou p = 37
1) Para p = 5 ---> m - k = 37 ---> x = 5.k
Participantes da 3ª edição ---> (x + 185 - 140)/p = (5.k + 45)/5 = k + 9 ---> inteiro ---> Não serve
2) Para p = 37 ---> m - k = 5 ---> x = 37.k ---> (37.k +45)/37 = m - k ---> k + 45/37 = m - k ---> m - 2k = 45/37
m - 2k = (45 + 29 - 29)/37 ---> m - 2k = (74 - 29)/37 ---> m - k = 2 - 29/37
Para a 4ª edição ser distribuída igualmente o menor aumento deverá ser 29

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Dúvida matemática
Re: Dúvida matemática
Elcioschin escreveu:Seja p o número de professores e x o número de participantes na 1ª edição: x/p = k ---> x = p.k ---> k inteiro ---> k > 0
Número de participantes na 2ª edição = x + 185 ---> (x + 185)/p = m ---> m inteiro ---> m > 0
(p.k + 185)/p = m ---> k + 185/p = m ---> 185/p = m - k ---> 5.37/p = m - k
Temos duas possibilidades ---> p = 5 ou p = 37
1) Para p = 5 ---> m - k = 37 ---> x = 5.k
Participantes da 3ª edição ---> (x + 185 - 140)/p = (5.k + 45)/5 = k + 9 ---> inteiro ---> Não serve
2) Para p = 37 ---> m - k = 5 ---> x = 37.k ---> (37.k +45)/37 = m - k ---> k + 45/37 = m - k ---> m - 2k = 45/37
m - 2k = (45 + 29 - 29)/37 ---> m - 2k = (74 - 29)/37 ---> m - k = 2 - 29/37
Para a 4ª edição ser distribuída igualmente o menor aumento deverá ser 29
Tive dúvida nessa questão também, não entendi a resolução nessas partes:
5.37/p = m - k: Essa é equação para a 2ª edição.
pq eu considero que p pode ser 5 ou 37 se esses valores estavam sendo divididos por p?
(x + 185 - 140)/p = (5.k + 45)/5 = k + 9 < pq k+9?
Laislilas- Jedi

- Mensagens : 435
Data de inscrição : 28/03/2014
Idade : 29
Localização : Salvador,Bahia,Brasil
 Re: Dúvida matemática
Re: Dúvida matemática
Nada foi considerado
O que foi feito na equação foi apenas fatorar 185 --> 185 = 5.37
5.37/p = k - m ---> Como k e m são inteiros e p também é, p SOMENTE pode ser 5 ou 37
(5.k + 45)/5 = (5.k)/5 + 45/5 = k + 9
O que foi feito na equação foi apenas fatorar 185 --> 185 = 5.37
5.37/p = k - m ---> Como k e m são inteiros e p também é, p SOMENTE pode ser 5 ou 37
(5.k + 45)/5 = (5.k)/5 + 45/5 = k + 9

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Dúvida matemática
Re: Dúvida matemática
eu entendi que foi fatorado mas a continuação não compreendi
Laislilas- Jedi

- Mensagens : 435
Data de inscrição : 28/03/2014
Idade : 29
Localização : Salvador,Bahia,Brasil
 Re: Dúvida matemática
Re: Dúvida matemática
Eu acabei de dar a explicação (na minha mensagem anterior).
Acho que você a leu tão rápido (que não parou para pensar)
Leia a explicação, desta vez, com atenção.
Acho que você a leu tão rápido (que não parou para pensar)
Leia a explicação, desta vez, com atenção.

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Dúvida matemática
Re: Dúvida matemática
Mestre Elcio, fiquei com dúvida na sua resolução.
Por que (37.k +45)/37 = m - k? Não entendi o motivo da 3ª edição ser a subtração dos valores inteiros da 2ª e 1ª edição.
Por que (37.k +45)/37 = m - k? Não entendi o motivo da 3ª edição ser a subtração dos valores inteiros da 2ª e 1ª edição.
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Re: Dúvida matemática
Re: Dúvida matemática
O produto dos dois fatores é 5.37
Se o primeiro fator equivale a 37, o segundo equivale a 5 ---> m - k = 5
Se o primeiro fator equivale a 37, o segundo equivale a 5 ---> m - k = 5

Elcioschin- Grande Mestre

- Mensagens : 73172
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Dúvida matemática
Re: Dúvida matemática
Eu não fui muito claro. Vou tentar explicar melhor a minha dúvida.
x=nº de provas
p=nº de professores
1ª Edição
x/p=k --> x=k.p
k=(nº de provas da 1ª edição)/(nº de professores) --> k deve ser inteiro.
2ª Edição
(x+185)/p=m
m=(nº de provas da 2ª edição)/(nº de professores) --> m deve ser inteiro.
x=k.p
(k.p+185)/p=m --> 185/p=m-k --> (5.37)/p=m-k
"p" só pode assumir 2 valores: 5 ou 37. Se p=5, então:
m-k=37 e x=k.5 ou m-k=5 e x=k.37
3ª Edição
(x+185-140)/p=q --> (k.p+45)/p=q --> k+45/p=q
q=(nº de provas da 3ª edição)/(nº de professores)
*As provas foram distribuídas desigualmente logo "q" não pode ser inteiro. Com isso, p=37 pois 45/5 torna "q" inteiro.
k+45/37=q
q=m-k ?(Eis a minha dúvida)
Segundo o senhor, k+45/37=m-k.
(nº pv. 3ª ed.)/(nº prof)=(nº pv. 2ª ed.)/(nº prof.)-(nº pv. 1ª ed.)/(nº prof.)
(nº pv. 3ª ed.)=(nº pv. 2ª ed.)-(nº pv. 1ª ed.) ???
x=nº de provas
p=nº de professores
1ª Edição
x/p=k --> x=k.p
k=(nº de provas da 1ª edição)/(nº de professores) --> k deve ser inteiro.
2ª Edição
(x+185)/p=m
m=(nº de provas da 2ª edição)/(nº de professores) --> m deve ser inteiro.
x=k.p
(k.p+185)/p=m --> 185/p=m-k --> (5.37)/p=m-k
"p" só pode assumir 2 valores: 5 ou 37. Se p=5, então:
m-k=37 e x=k.5 ou m-k=5 e x=k.37
3ª Edição
(x+185-140)/p=q --> (k.p+45)/p=q --> k+45/p=q
q=(nº de provas da 3ª edição)/(nº de professores)
*As provas foram distribuídas desigualmente logo "q" não pode ser inteiro. Com isso, p=37 pois 45/5 torna "q" inteiro.
k+45/37=q
q=m-k ?(Eis a minha dúvida)
Segundo o senhor, k+45/37=m-k.
(nº pv. 3ª ed.)/(nº prof)=(nº pv. 2ª ed.)/(nº prof.)-(nº pv. 1ª ed.)/(nº prof.)
(nº pv. 3ª ed.)=(nº pv. 2ª ed.)-(nº pv. 1ª ed.) ???
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Re: Dúvida matemática
Re: Dúvida matemática
"Uma mesma equipe, com menos de 50 professores[4], corrigiu 3 edições de um exame, tendo sido possível dividir[1] as provas igualitariamente entre eles nas duas primeiras, mas não na terceira[2]". Da 1º para a 2º edição, o número de provas aumentou 185[3], mas da 2º para a 3º, houve uma redução de 140[5]. Para uma 4º edição, o menor aumento nesse número, para que volte a ser possível distribuí-las por igual é:
[1] K inteiro na primeira edição.
[2] Só aceita fração irredutível na terceira edição.
[3] A quantidade total de provas não definida é x. Se o número de provas aumentou: x+185. Obs: O número de participantes e de provas são iguais, porque o enunciado não informa o número de faltantes.
Razão: número de participantes/número de professores = K --> (x+185)/p = m.
[4] O número de professores é inteiro(2~49).
[5] Redução de 140 provas em x+185. A nova razão é x + 185 - 140/p
p é o número de professores
x é o número de participantes
A razão número de participantes/número de professores é K
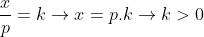
[1] Razão é K é inteiro.
"o número de provas aumentou 185". A Razão número de participantes/número de professores é m.

Para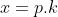
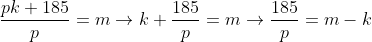
Passei o K para o outro lado e ficou -k.
m-k é a subtração: razão da 1ª edição menos razão da 2ª edição.
Para encontrar os possíveis valores de p:
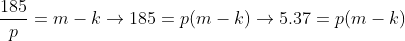
Por igualdade: p = 5 ou p = 37
(m - k) = 5 ou (m - k) = 37
x = 5k ou x= 37k
Para p = 5 e x = 5k
(m - k) = 5
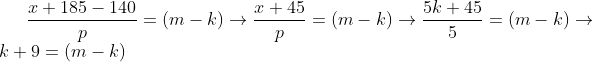
K+9 é número inteiro.(Não serve)
Para p = 37 e x = 37k
(m - k) = 37
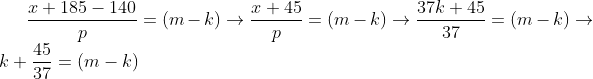
k+45/37 é fração irredutível.(Serve)
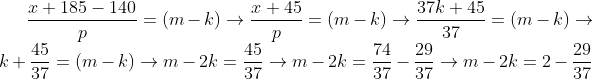
[1] K inteiro na primeira edição.
[2] Só aceita fração irredutível na terceira edição.
[3] A quantidade total de provas não definida é x. Se o número de provas aumentou: x+185. Obs: O número de participantes e de provas são iguais, porque o enunciado não informa o número de faltantes.
Razão: número de participantes/número de professores = K --> (x+185)/p = m.
[4] O número de professores é inteiro(2~49).
[5] Redução de 140 provas em x+185. A nova razão é x + 185 - 140/p
1ª edição (aceita número inteiro):
Dados:p é o número de professores
x é o número de participantes
A razão número de participantes/número de professores é K
[1] Razão é K é inteiro.
2ª edição(aceita número inteiro)
"o número de provas aumentou 185". A Razão número de participantes/número de professores é m.
Para
Passei o K para o outro lado e ficou -k.
m-k é a subtração: razão da 1ª edição menos razão da 2ª edição.
Para encontrar os possíveis valores de p:
Por igualdade: p = 5 ou p = 37
(m - k) = 5 ou (m - k) = 37
x = 5k ou x= 37k
3ª edição(Só aceita fração irredutível):
Redução de 140 provas em x+185. A nova razão é x + 185 - 140/pPara p = 5 e x = 5k
(m - k) = 5
K+9 é número inteiro.(Não serve)
Para p = 37 e x = 37k
(m - k) = 37
k+45/37 é fração irredutível.(Serve)
Convidado- Convidado
Página 1 de 2 • 1, 2 
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












