IME 2011

Seja p(x) uma função polinomial satisfazendo a relação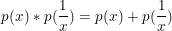  
Sabendo que p(3) = 28, o valor de p(4) é:

a) 10
b) 30
c) 45
d) 55
e) 65

A questão não é a resolução da questão em si, e sim uma dúvida minha sobre as resoluções propostas nos sites do poliedro ( http://www.sistemapoliedro.com.br/poliedroresolve/IME/2011/ ) e farias brito(questão 11 da prova objetiva) (http://www.fariasbrito.com.br/sistemas/comentario/index.php?vestibular=16).

Ambos usaram do argumento de que p(x) era recíproco devido ao fato de se 'r' é uma raiz de p(x),ou seja, p(r)=0 , temos que p(1/r)=0. Contudo, para ser reciproco, não é necessário garantir que 'r' e '1/r' sejam raízes com a mesma multiplicidade? Pois só assim (se tiverem a mesma multiplicidade) que se tem um polinômio da forma  ..um exemplo onde não se tem a mesma multiplicidade, e portanto não é da forma ao lado, é 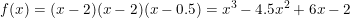, embora ocorra f(2)=f(0.5)=0.

Ou seja, minha dúvida é se esta certo partir pra premissa que o polinômio é reciproco, como fizeram os sites acima.

Obs 1:Outros sites resolveram sem se utilizar desse argumento de reciprocidade.
Obs 2: O livro do Aref e do Iezzi ressaltam o fato de que para a  ser recíproca, é necessário se ter mesma multiplicidade, em quanto o livro do Caio Guimarães diz apenas que se 'r' e '1/r' atendem a equação(no caso,se são raízes), então a equação é reciproca.

Gostaria do auxílio de vocês para esclarecer esse assunto. Grato.

Cara, calma , entendo muito bem esse ''tipo'' de dúvida, que na verdade é isso mesmo, afinal os cursinhos adoram resumir suas soluções da internet.
Eu não acessei os links mas não dá pra determinar o grau do polinômio usando apenas essa equação dada pelo enunciado, então você vai ter sim que admitir que é recíproca, é só observar pela equação, prova do IME tem que ter malícia, espero ter ajudado.

Opa,então, quando vi a resolução dos sites acima cheguei a pensar que teria que partir desse pressuposto para conseguir resolver a questão, mas essa resolução que vi depois no site 'rumo ao ita'  eu achei mais justa:



Nesse caso, não foi necessário admitir que o polinômio fosse recíproco.Por existir uma solução que não partiu dessa premissa é o que me levou a pensar que esses sites deram um "chute" inicial de que p(x) era recíproco e acabaram achando o polinômio que satisfaz o problema, rsrs