Tartaglia (Eq.3° grau)
3 participantes
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
 Tartaglia (Eq.3° grau)
Tartaglia (Eq.3° grau)
Vou colocar aqui a demonstração da simpática fórmula de Tartaglia para obter raízes de uma equação de 3° grau desprovida de termos de 2° grau, do tipo:
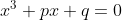
Vamos conjecturar que as raízes reais sejam da forma:
![x=\sqrt[3]{a}+\sqrt[3]{b}](https://latex.codecogs.com/gif.latex?x=\sqrt[3]{a}+\sqrt[3]{b})
Elevando ao cubo temos:
![x^3=a+b+3 \sqrt[3]{ab}(\sqrt[3]{a}+\sqrt[3]{b})](https://latex.codecogs.com/gif.latex?x^3=a+b+3&space;\sqrt[3]{ab}(\sqrt[3]{a}+\sqrt[3]{b}))
Perceba que a parcela entre parênteses é igual ao próprio x, passando todos os termos para um só lado temos que:
![x^3 -(a+b)-3 \sqrt[3]{ab}x=0](https://latex.codecogs.com/gif.latex?x^3&space;-(a+b)-3&space;\sqrt[3]{ab}x=0)
Logo:
![x^3 -(a+b)-3 \sqrt[3]{ab}x\equiv x^3+px+q](https://latex.codecogs.com/gif.latex?x^3&space;-(a+b)-3&space;\sqrt[3]{ab}x\equiv&space;x^3+px+q)
Por consequência:
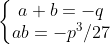
Podemos dizer que a e b são raízes da equação:

Sendo assim temos as raízes reais de equações do tipo:
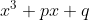
Podem ser escritas como:
![x=\sqrt[3]{q/2+\sqrt[]{q^2+4p^3/27}/2}+ \sqrt[3]{q/2-\sqrt[]{q^2+4p^3/27}/2}](https://latex.codecogs.com/gif.latex?x=\sqrt[3]{q/2+\sqrt[]{q^2+4p^3/27}/2}+&space;\sqrt[3]{q/2-\sqrt[]{q^2+4p^3/27}/2})
Prefiro Girard, .
.
Vamos conjecturar que as raízes reais sejam da forma:
Elevando ao cubo temos:
Perceba que a parcela entre parênteses é igual ao próprio x, passando todos os termos para um só lado temos que:
Logo:
Por consequência:
Podemos dizer que a e b são raízes da equação:
Sendo assim temos as raízes reais de equações do tipo:
Podem ser escritas como:
Prefiro Girard,

jango feet- Matador

- Mensagens : 476
Data de inscrição : 30/01/2013
Idade : 29
Localização : Feira de santana;Bahia, Brasil
Hater1212 gosta desta mensagem
 Equação do 3º grau
Equação do 3º grau
jango feet escreveu:Vou colocar aqui a demonstração da simpática fórmula de Tartaglia para obter raízes de uma equação de 3° grau desprovida de termos de 2° grau, do tipo:
Vamos conjecturar que as raízes reais sejam da forma:
Elevando ao cubo temos:
Perceba que a parcela entre parênteses é igual ao próprio x, passando todos os termos para um só lado temos que:
Logo:
Por consequência:
Podemos dizer que a e b são raízes da equação:
Sendo assim temos as raízes reais de equações do tipo:
Podem ser escritas como:
Prefiro Girard,.
Este método é melhor:
Fazendo:
e
Tem-se:
Exemplo:
Seja a equação:
Neste caso:
a = 1
b = -6
c = 11
d = -6
Substituindo valorese realizando operações, vem:
x1 = 2
x2 = 3
x3 = 1
Resolvendo pelo Wolfram-Alpha os valores batem, o que valida o método.
O método está em https://problemasteoremas.wordpress.com/2010/05/13/resolucao-da-equacao-do-3-%C2%BA-grau-ou-cubica/
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 74
Localização : Vitória, ES.
Hater1212 gosta desta mensagem
 Re: Tartaglia (Eq.3° grau)
Re: Tartaglia (Eq.3° grau)
Pode-se deduzir ainda uma outra expressão para resultados gerais para um polinômio de 3º grau qualquer. Utilizando o útil resultado: " Dada a equação transformatriz 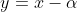 , responsável por eliminar o termo de k-ésimo grau de
, responsável por eliminar o termo de k-ésimo grau de =a_{n}.x^{n}+a_{n-1}.x^{n-1}+a_{n-2}.x^{n-2}+...+a_{1}.x+a_{0}) , então ''Alfa'' é raiz da k-ésima derivada de p(x) com relação a x ". Utilizando esse fato, podemos fazer com que a transformada aditiva
, então ''Alfa'' é raiz da k-ésima derivada de p(x) com relação a x ". Utilizando esse fato, podemos fazer com que a transformada aditiva ) seja desprovida de termo do segundo grau, caindo assim num Polinômio que respeita as condições de Targaglia-Cardano, cujas raízes serão em y, bastando adicionar à expressão de Tartaglia o termos ''Alfa'' encontrado, tendo assim, uma expressão assim como a de Báskara que fornece as raízes de p(x)=a.x³+b.x³+c.x+d. Assim como a expressão utilizada pelo Luiz, ela não é útil em nenhuma prova, tanto que não é ensinada em nenhum livro ou escola, justamente por tomar muito tempo e espaço, mesmo fornecendo as raízes de p(x). Fica a cargo de curiosidade
seja desprovida de termo do segundo grau, caindo assim num Polinômio que respeita as condições de Targaglia-Cardano, cujas raízes serão em y, bastando adicionar à expressão de Tartaglia o termos ''Alfa'' encontrado, tendo assim, uma expressão assim como a de Báskara que fornece as raízes de p(x)=a.x³+b.x³+c.x+d. Assim como a expressão utilizada pelo Luiz, ela não é útil em nenhuma prova, tanto que não é ensinada em nenhum livro ou escola, justamente por tomar muito tempo e espaço, mesmo fornecendo as raízes de p(x). Fica a cargo de curiosidade  .
.

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» funcao do primeiro grau e segundo grau
» Polinômio do 3º grau para 2º grau
» Eq do 2nd grau
» Eq do 2nd grau 02
» Eq. do 2° Grau
» Polinômio do 3º grau para 2º grau
» Eq do 2nd grau
» Eq do 2nd grau 02
» Eq. do 2° Grau
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|













