Área do trapézio
2 participantes
Página 1 de 1
 Área do trapézio
Área do trapézio
ABC é um triãngulo inscrito num círculo de raio 3 m, cujos lados AC e BC são respectivamente iguais aos lados do quadrado e do triângulo equilátero inscritos. O diâmetro paralelo ao lado BC intercepta os lados AB e AC nos pontos M e N, respectivamente. Calcular a área do trapézio BMNC.
[justify]Resposta: 6,37 m²

Fafa- Grupo
Velhos amigos do Fórum
- Mensagens : 497
Data de inscrição : 31/07/2009
Localização : Rio de Janeiro
 Re: Área do trapézio
Re: Área do trapézio
Olá, Fafa.

Sendo BC lado de um triângulo equilátero inscrito teremos:
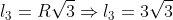
De maneira análoga para o lado AC teremos:
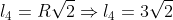
Utilizando a lei dos senos temos:
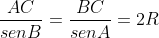
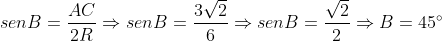
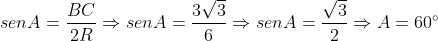
=\frac{1}{2}.\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}=\frac{\sqrt{2}+\sqrt{6}}{4})
Cálculo da área do triângulo ABC.
}{8}\Rightarrow A=\frac{9\sqrt{3}+27}{4})
Calculo da altura AH.
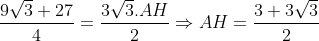
A altura do trapézio MNBC é igual ao apótema do triângulo equilátero de base BC pois, o diâmetro do círculo passa pelos pontos M e N, que é paralelo a BC.
Cálculo da altura do trapézio.

A altura do triângulo do triângulo AMN é igual a (AH-x).

Sendo os triângulos ABC e ABN semelhantes a razão entre suas é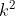 , ou seja igual ao quadrado da razão de semelhança.
, ou seja igual ao quadrado da razão de semelhança.
^2=\frac{6-3\sqrt{3}}{2}\Rightarrow A_{AMN}=A_{ABC}.\frac{6-3\sqrt{3}}{2})

Logo, a área do trapézio MNBC será:

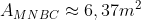

Sendo BC lado de um triângulo equilátero inscrito teremos:
De maneira análoga para o lado AC teremos:
Utilizando a lei dos senos temos:
Cálculo da área do triângulo ABC.
Calculo da altura AH.
A altura do trapézio MNBC é igual ao apótema do triângulo equilátero de base BC pois, o diâmetro do círculo passa pelos pontos M e N, que é paralelo a BC.
Cálculo da altura do trapézio.
A altura do triângulo do triângulo AMN é igual a (AH-x).
Sendo os triângulos ABC e ABN semelhantes a razão entre suas é
Logo, a área do trapézio MNBC será:
adriano tavares- Grande Mestre

- Mensagens : 600
Data de inscrição : 25/07/2009
Localização : São Paulo
 Re: Área do trapézio
Re: Área do trapézio
Obrigada Adriano.

Fafa- Grupo
Velhos amigos do Fórum
- Mensagens : 497
Data de inscrição : 31/07/2009
Localização : Rio de Janeiro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












