Relações Métricas

por Diego Reis Sex 26 Set 2014, 20:05

Na figura, as circunferências têm raios iguais a R e estão inscritas em um triângulo equilátero de lado 2cm. Assinale a alternativa que representa o valor de R.

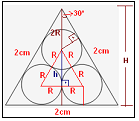
A resposta é 1/1+√3 cm

Eu sei que:
2R+h+R=H
3R+R√3=√3

Chega aqui me embolo pois eu faço o seguinte:
2R = √3/3+√3

E agora ?

por **raimundo pereira** Sex 26 Set 2014, 20:34

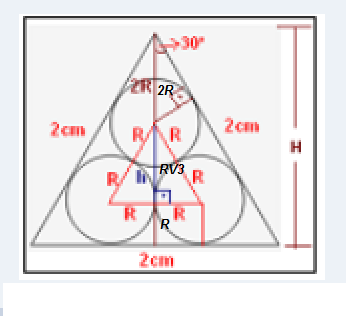
No triângulo retângulo 30/60/90, o menor cateto mede a metade da hipotenusa e o maior cateto é igual ao menor vezes a V3.

Assim, temos que a altura do triângulo maior é: 1. V3= V3 (menor cateto vezes a V3) e, a altura do menor triângulo é : R.V3 ( menor cateto vezes V3).

Então a altura do triângulo grande fica: 2R+RV3+R= V3-->3R+RV3=V3-->R(3+V3)=V3
R=V3(3-V3)/(3+V3).(3-V3)=(V3-1)/2

por Diego Reis Sex 26 Set 2014, 22:19

Mas o gabarito é 1/1+v3 ...

Eu fiz quase isso, fiz assim:
Eu sei que:
2R+h+R=H
3R+R√3=√3

Ai agora eu ví que pode por em evidência, como o sr. fez:
R(3+√3)=√3
R=√3/3+√3

Até ai deu; mas como poderia achar 1/1+√3 ?