OBF 2007 3ª Fase Refração 2

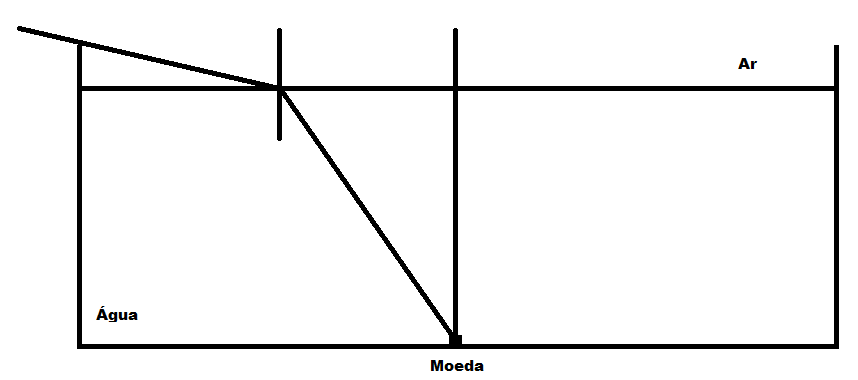
(OBF 2007 -3ª fase) Uma moeda se encontra exatamente na parte central do fundo de um tanque de água montado sobre a carroceria de um caminhão. Um rapaz que observa a moeda, segundo um ângulo α em relação à normal à superfície do líquido, mede uma profundidade aparente de 50 cm. Em certo instante o caminhão se move para frente com aceleração constante e o rapaz, observando a moeda com o mesmo ângulo α em relação à normal à superfície do líquido (que agora está inclinada), atribui uma profundidade aparente de 25*(raiz de 3) cm. Determine a aceleração do caminhão.

Spoiler:

Fala, Diego.
A geometria é pesada.

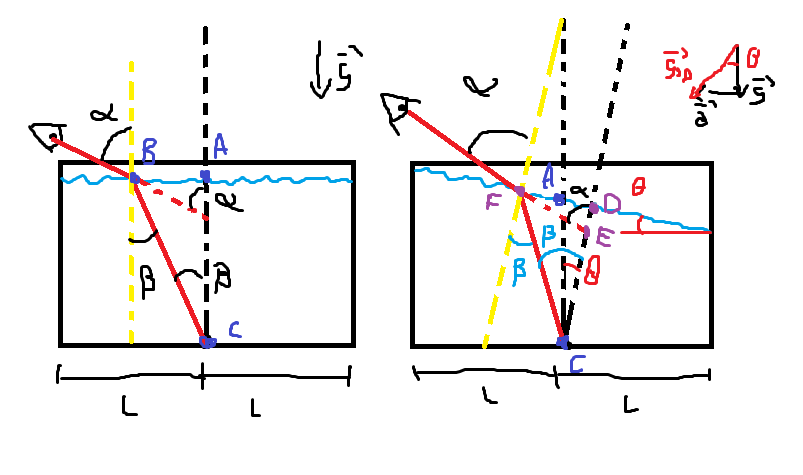
Na esquerda temos a situação sem o caminhão acelerar e na direita temos a situação em que ele acelera. Primeiro, ao acelerar vamos definir o ângulo theta como sendo o ângulo entre a gravidade aparente (soma vetorial da gravidade com a aceleração gerada pela inércia do movimento) e a gravidade real da Terra de tal forma que tg(theta) = a/g.

Dito isso, temos também que ter em mente que a superfície da água se alinha com a gravidade aparente formando 90 graus com ela e, por consequência disso, o ângulo theta está entre a direção perpendicular ao chão do vagão e a direção perpendicular à superfície do líquido (são as duas retas pretas no desenho da direita) como mostra a imagem .

Pensando agora no desenho da esquerda, sendo alpha o ângulo entre a normal e o ângulo de visão como disse a questão e beta o ângulo entre o raio incidente e a normal, temos que a reta preta AC é paralela a reta amarela pois as duas retas são perpendiculares ao chão do vagão. Sendo assim, pelas condições do paralelismo, alocamos alpha e beta nas posições mostradas do triangulo ACB. Logo:
tg(alpha) = AB/(profundidade aparente)
tg(beta) = AB/(profundidade real)
dividindo uma pela outra:
tg(alpha)/tg(beta) = Profundidade Real/Profundidade aparente = P1/Pa1. (i)

Analogamente, pelas condições de paralelismo, chegamos a mesma conclusão para a situação na direita (olhe para os triângulos FDE e FCD):
tg(alpha)/tg(beta) = Profundidade Real(DC)/Profundidade aparente(DE) = P2/Pa2. (ii)

(i) = (ii):
P2/Pa2 = P1/Pa1
DC/25√3 = AC/50
DC/AC = √3/2

Agora, repare que DC/AC é igual ao cosseno de theta (como a moeda está no ponto médio, a medida AC não muda devido ao movimento do líquido)

Assim: cos(theta) = √3/2 -> theta = 30 graus

Então sua tangente vale √3/3

Como tg(theta) = a/g -> a = √3g/3.

UFA