número binomial

se K é a quantidade de números ímpares compreendidos entre 5000 e 9000 que se pode formar utilizando somente os algarismos 5, 6, 7 e 9, de modo que não figurem algarismos repetidos, então o números binomial .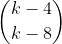




Re- 210.



estava respondendo por restrição:
qualquer número formado entre 5000 e 9000 possuem 4 algarismos entao por restrição temos::
o 1° não pode ser9
assim, temos 3 opções para o 1°,
3 opções para o 2° pois ja pode usar o 9 e excluir usado no anterior,
para o 3° 2 opções excluindo os utilizados anteriormente e por fim 1 opção para o ultimo, mas sabendo que pode ser qualquer um pois dispomos de algarismos ímpares.
assim teremos no total
3*3*2*1=18
assim teremos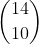 = 1001 e não coincide com o gabarito, onde estou errando?

Olá.

Começados por 5:

5 _ _ _ --> Deve ser terminado em 7 ou 9. Terminado em 7: 5 _ _ 7 --> 2 possibilidades. Terminado em 9: 5_ _ 9 --> 2 possibilidades

Começados por 6:

6 _ _ _ --> Terminado em 5: 2 possibilidade, Terminado em 7: 2 possibilidades, Terminado em 9: 2 possibilidades

Começados por 7:

7 _ _ _ --> Terminados em 5: 2 possibilidades, Terminados em 9: 2 possibilidades

Total: 14

C10,6 = (10*9*8*7*6!)/(6!4!) .:. (10*9*8*7)/24 .:. 210

Att.,
Pedro

ótimo e simples!