Lados do Triângulo em P.G

por matheusenra Qua 05 Mar 2014, 17:01

As medidas dos lados de um triângulo estão em Progressão Geométrica, a razão dessa progressão não pode ser o número:

a) 1/2
b) 2/3
c) 3/4
d) 4/5
e) 5/6

GABARITO:

por Dela Corte Qua 05 Mar 2014, 17:43

Temos um triângulo qualquer de lados (a,b,c). Como eles estão em uma PG,
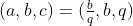
$Lados do Triângulo em P.G Gif$
onde q é a razão da PG.

Teremos, para a condição de existência do triângulo, que

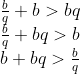
$Lados do Triângulo em P.G Gif$

Como nem b nem q podem ser zero, vamos dividir as equações por b e multiplicá-las por q, facilitando a resolução.

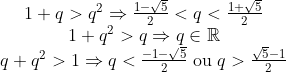
$Lados do Triângulo em P.G Gif$

Fazendo a união dos conjuntos, teremos

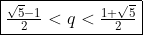
$Lados do Triângulo em P.G Gif$

O único valor que não se encontra nesse intervalo é 1/2.

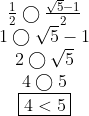
$Lados do Triângulo em P.G Gif$

Alternativa A.

por Luck Qua 05 Mar 2014, 17:45

Seja a , aq , aq² os lados do triângulo , q > 0 .

|aq - a |< aq² < a + aq (desigualdade triangular)
aq² < a + aq
q² - q - 1 < 0
(1-√5)/2 < q< (1+√5)/2 ∴ 0 < q < 1,61 (aproximado)

|aq -a | < aq² , se 0 < q < 1 :
-(aq -a) < aq²
q² + q - 1 > 0
q < (-1-√5)/2 (não convém) ou q > (√5-1)/2 ∴ q > 0,61 (aproximado) , o que já elimina q = 1/2 , letra a.

por **ivomilton** Qua 05 Mar 2014, 17:55

matheusenra escreveu:As medidas dos lados de um triângulo estão em Progressão Geométrica, a razão dessa progressão não pode ser o número:

a) 1/2
b) 2/3
c) 3/4
d) 4/5
e) 5/6

GABARITO:

Boa tarde, Matheus.

"O maior lado de um triângulo deve ser menor que a soma dos outros dois."

:: a : b : c

Testando as alternativas:

a) q = 1/2

q = b/a = 1/2

a = 2b

q = c/b = 1/2

b = 2c

E a PG seria assim formada:

:: 2b : b
:: __ : 2c : c

.. 4c : 2c : c

Aplicando-se a regra:
4c < 2c + c
4c < 3c ??

Logo, a alternativa (a) já não pode ser.

Um abraço.