Provar que
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Provar que
por Pietro di Bernadone Seg 17 Jun 2013, 16:44
Prove que se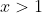 
então as potências sucessivas 
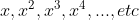, crescem e podem vir a superar qualquer número fixado de antemão. Mais precisamente se 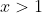então, dado qualque 
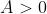, é possível obter um inteiro 
tal que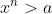 
.
Pietro di Bernadone- Grupo
Velhos amigos do Fórum
- Mensagens : 1344
Data de inscrição : 04/03/2010
Idade : 34
Localização : Rio de Janeiro
Re: Provar que
por JOAO [ITA] Ter 18 Jun 2013, 16:06
Vou demonstrar por redução ao absurdo.
Supondo que não exista nenhum inteiro 'n' tal que x^n > A para x > 1 e A > 0 então todos os n's possuem a propriedade x^n ≤ A, já que se um número não é maior que outro ele só pode ser menor ou igual.
Ora, mas essa última condição deixa implícito que existe algum inteiro máximo dentro do conjunto dos números inteiros o que, pelo Princípio da Boa Ordenação, é inviável.
C.q.d
Supondo que não exista nenhum inteiro 'n' tal que x^n > A para x > 1 e A > 0 então todos os n's possuem a propriedade x^n ≤ A, já que se um número não é maior que outro ele só pode ser menor ou igual.
Ora, mas essa última condição deixa implícito que existe algum inteiro máximo dentro do conjunto dos números inteiros o que, pelo Princípio da Boa Ordenação, é inviável.
C.q.d
![JOAO [ITA]](https://2img.net/u/2713/85/25/58/avatars/20221-80.jpg)
JOAO [ITA]- Fera
- Mensagens : 866
Data de inscrição : 25/02/2012
Idade : 27
Localização : São José dos Campos,SP,Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
