Provar m^5-m | 30

por Smasher Sex 12 Jun 2015, 17:05

Provar que 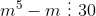$Provar m^5-m | 30 Gif$

para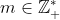 $Provar m^5-m | 30 Gif$

Tentei provar separadamente por 2, por 3 e por 5, mas só consegui para 2 e para 3.

Obg :face:

por Luck Sex 12 Jun 2015, 19:27

Para provar que é divisível por 5, vc pode usar o corolário do teorema de Fermat:
m^p ≡ m mod(p) , sendo m ∈ ℤ*+ e p primo.
então m^5 ≡ m mod(5) ∴ m^5 - m ≡ 0 mod(5)
Também dá para provar por indução..

por **Carlos Adir** Sex 12 Jun 2015, 19:32

É para provar através de congruência ou por indução?
Por indução é mais fácil:
$\\ \mathrm{Seja \ m=2, \ ent\~ao:} \\ \mathrm{m^5-m=2^5-2=30} \\ \mathrm{Logo, \ para \ m=2 \ d\'a \ certo} \\ \mathrm{Supomos \ que \ m^5-m=30k, \ k \in \mathbb{Z}} \\ \mathrm{Se \ vale \ para \ todo \ m \in \mathbb{Z}_{+}^{*}, \ ent\~ao \ vale \ para \ m+1:} \\ \mathrm{(m+1)^5-(m+1)=m^5 + 5m^4 + 10m^3 +10m^2 + 5m+1-m-1 } \\ \mathrm{=( m^5-m)+5m(m^3 + 2m^2+2m+1)= 30k+5m \left(m^3+m^2+(m+1)^2 \right )} \\ \mathrm{=5[6k + m \left(m+1 \right )(m^2+m+1)]}$
Agora, devemos provar que m(m+1)(m²+m+1) é multiplo de 6. E pra isso, devemos provar que tal número é multiplo de 2 e 3 ao mesmo tempo.
Fica fácil verificar, se m for impar, então (m+1) é par, e faz com que o termo seja multiplo de 2.
E do mesmo modo, se m for par, o número já fica multiplo de 2.
Agora, devemos provar que m(m+1)(m²+m+1) é multiplo de 3.
Se m ou m+1 for multiplos de 3, então não há nada com que nos preocupar. Contudo, se nenhum deles for multiplo de 3, teremos problemas.
Então, vamos considerar m = 3t+1 ---> m+1=3t+2, ou seja, nenhum é multiplo de 3.
Colocando m=3t+1, obtemos:
$\\ \mathrm{=5[6k + m \left(m+1 \right )(m^2+m+1)]} \\ \mathrm{=5 \left[6k+(3t+1)(3t+2)\left[(3t+1)^2+(3t+1)+1 \right ] \right ]} \\ \mathrm{=5 \left[6k+(3t+1)(3t+2) \left(9t^2+9t+3 \right ) \right ]} \\ \mathrm{=5 \left[6k+3(3t+1)(3t+2)(3t^2+3t+1) \right ]}$

Logo, vale para todo m inteiro.

Há maneira de provar através de congruência também.

por **Adeilson** Sex 12 Jun 2015, 19:36

OBS.: A notação correta é 30|(m^5-m)
Vou fazer de uma forma não muito elegante, mas que é válida.
m^5-m=m(m^4-1)=(m-1)m(m+1)(m²+1) daqui você já tira que, como temos o produtos de três números consecutivos, a expressão é divisível por 2 e por 3, basta mostrarmos agora que também é divisível por 5.
fazendo por indução em m, teremos:
m=1 -> m^5-m=0 e 30|0 OK!
suponha que m^5-m=5k, para algum k inteiro, então devemos ter (m+1)^5-(m+1)=5t, para algum t inteiro, vejamos:
(m+1)^5-(m+1)=m^5+5m^4+10m³+10m²+4m=m^5-m+5m^4+10m³+10m²+4m+m=5k+5(m^4+2m³+2m²+1) que é divisível por 5 e terminamos a demonstração.

por **Adeilson** Sex 12 Jun 2015, 19:38

Nossa, todos juntos Laughing

kkkk

por Smasher Sex 12 Jun 2015, 19:42

Boa Noite, muito obrigado por todas as respostas.
Carlos Adir, poderia demonstrar como fazer por congruência? Nunca vi resolução igual, então, se possível, agradeceria muito :-)

por **Carlos Adir** Sex 12 Jun 2015, 20:12

A por congruência é a que o o Luck usou, que matou a questão.
Para provar por 2:
$\\ \mathrm{m \equiv 0 \pmod {2} \Rightarrow m^5 \equiv 0^5 \pmod{2} \Rightarrow m^5-m \equiv 0 \pmod{2}} \\ \mathrm{m \equiv 1 \pmod{2} \Rightarrow m^5 \equiv 1^5 \pmod{2} \Rightarrow m^5 -m \equiv 0 \pmod{2}}$
Para provar por 3:
$\\ \mathrm{m \equiv 0 \pmod {3} \Rightarrow m^5 \equiv 0^5 \pmod{3} \Rightarrow m^5-m \equiv 0 \pmod{3}} \\ \mathrm{m \equiv 1 \pmod{3} \Rightarrow m^5 \equiv 1^5 \pmod{3} \Rightarrow m^5 -m \equiv 0 \pmod{3}} \\ \mathrm{m \equiv 2 \pmod{3} \Rightarrow m^5 \equiv 2^5 \pmod{3} \Rightarrow m^5 - m \equiv 0 \pmod{3}}$
Para provar por 5:
$\\ \mathrm{m \equiv 0 \pmod {5} \Rightarrow m^5 \equiv 0^5 \pmod{5} \Rightarrow m^5-m \equiv 0^5 - 0 \equiv 0 \pmod{5}} \\ \mathrm{m \equiv 1 \pmod {5} \Rightarrow m^5 \equiv 1^5 \pmod{5} \Rightarrow m^5-m \equiv 1^5 - 1 \equiv 0 \pmod{5}} \\ \mathrm{m \equiv 2 \pmod {5} \Rightarrow m^5 \equiv 2^5 \pmod{5} \Rightarrow m^5-m \equiv 2^5 - 2 \equiv 0 \pmod{5}} \\ \mathrm{m \equiv 3 \pmod {5} \Rightarrow m^5 \equiv 3^5 \pmod{5} \Rightarrow m^5-m \equiv 3^5 - 3 \equiv 0 \pmod{5}} \\ \mathrm{m \equiv 4 \pmod {5} \Rightarrow m^5 \equiv 4^5 \pmod{5} \Rightarrow m^5-m \equiv 4^5 - 4 \equiv 0 \pmod{5}}$
Assim, é multiplo por 30.

Luck usou um teorema muito importante, que diz:
$\\ \mathrm{m^{p-1} \equiv 1 \pmod{p} \Leftrightarrow p \ \'e \ primo, \ mdc(m, \ p)=1} \\ \mathrm{Ent\~ao:} \\ \mathrm{m^{5-1} \equiv 1 \pmod{5} \Rightarrow m^4 \equiv 1 \pmod{5} \Rightarrow} \\ \mathrm{m\left(m^4 \right ) \equiv m \left(1 \right ) \pmod{5} \Rightarrow m^5 \equiv m \pmod{5}} \\ \boxed{\mathrm{\therefore m^5 - m \equiv 5}}$

E gostei da resolução do Adeilson, fatorar foi uma solução muito boa.