Cônicas
3 participantes
Página 1 de 1
Cônicas
por rodrigo.correa Sex 14 Jun 2013, 20:08
Um holofote situado na posição (-5,0) ilumina uma região elíptica de contorno x² + 4y² = 5, projetando sua sombra numa parede representada pela reta x = 3, conforme ilustra a figura abaixo.
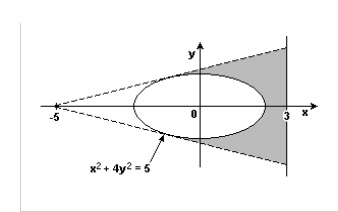
Considerando o metro a unidade dos eixos, o comprimento da sombra projetada é de:
a) 2
b) 3
c) 4
d) 5
Considerando o metro a unidade dos eixos, o comprimento da sombra projetada é de:
a) 2
b) 3
c) 4
d) 5
rodrigo.correa- Iniciante
- Mensagens : 1
Data de inscrição : 17/04/2012
Idade : 30
Localização : Barcarena, Pará, Brasil
Re: Cônicas
por Elcioschin Sex 14 Jun 2013, 21:46
Reta que passa por (-5, 0) e com coeficiente angular m ----> y - 0 = m.(x + 5) ----> y = mx + 5m
Pontos de contato com a elipse: x² + 4.(mx + 5m)² = 5 ----> (4m² + 1).x² + 40m²x + (100m² - 5) = 0
Para haver apenas 1 ponto de contato com cada reta ----> ∆ = 0 --->(40m²)² - 4.(4m² + 1).(100m² - 5) = 0
1600.(m²)² + 1600.(m²)² + 320.m² - 20 = 0 ---->160.(m²)² + 16.m² - 1 = 0
Calculado m determine os dois pontos de contato A(xA, yA) e B(xA, - yA)
Depois faça semelhança de triângulos:
(xA + 5)/2.yA = (3 + 5)/S ----> Calcule o comprimento S da sombra
Pontos de contato com a elipse: x² + 4.(mx + 5m)² = 5 ----> (4m² + 1).x² + 40m²x + (100m² - 5) = 0
Para haver apenas 1 ponto de contato com cada reta ----> ∆ = 0 --->(40m²)² - 4.(4m² + 1).(100m² - 5) = 0
1600.(m²)² + 1600.(m²)² + 320.m² - 20 = 0 ---->160.(m²)² + 16.m² - 1 = 0
Calculado m determine os dois pontos de contato A(xA, yA) e B(xA, - yA)
Depois faça semelhança de triângulos:
(xA + 5)/2.yA = (3 + 5)/S ----> Calcule o comprimento S da sombra
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Cônicas
por Rafafireman Seg 06 Out 2014, 10:29
Calculei m e achei +ou-1/4 . Dai em diante nao consigo desenvolver os pontos de contato nem a semelhança de triângulos .Se puder me ajudar agradeço desde já ,Obrigado!
Rafafireman- Iniciante
- Mensagens : 23
Data de inscrição : 10/10/2013
Idade : 42
Localização : Rio de janeiro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
