Equilíbrio dos corpos extensos

por Leonardo Rêgo Quirino Qua 06 Jun 2012, 18:24

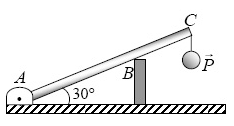
No arranjo da figura a seguir, uma barra rígida AC, de peso desprezível apoiada numa estaca fixa vertical em B, sustenta um peso P = 80√3 N. Conhecidas as distâncias AC = 80 cm, BC = 30 cm e estando o sistema em equilíbrio estático, calcule o módulo:
a) da reação da estaca na barra em B;
b) das componentes horizontal e vertical da reação de A na barra AC.

Equilíbrio dos corpos extensos Figura

OBS: minhas falhas principais são encontrar as forças que participam desse conjunto, obrigado. Very Happy

por **Elcioschin** Qua 06 Jun 2012, 19:01

Atuam as seguintes forças

1) No apoio A: Força horizontal Rh para a direita e força vertical Rv (para baixo)

2) No ponto B: Reação normal N perpendicular à barra, (inclinada, para cima à esquerda)

3) Peso P indicado

Projete a força N em eixo horizontal (Nh, para a esquerda) e num vertical (Nv, para cima)
Projete a força P (Py) num eixo perpendicular à barra (inclinado para a direita) e no eixo da barra (Px, sentido para o ponto A).

Nh = N*cos60º ---- Nv = N*cos30º -----> Px = P*cos60º = (80*\/3)*(1/2) Px = 40*\/3 -----> Py = P*cos30º = (80*\/3)*(\/3/2) = 120

Monte as equações de equlíbrio:

a)Momento em relação ao apoio A: N*(8 - 3) = Py*8 ----> N*5 = 120*8 ----> N = 192 N

b) Equlíbrio nos eixos vertical e horizontal

Rh = Nh ----> Rh = N*cos60º ----> Rh = 192*(1/2) ----> Rh = 96 N

Rv + P = Nv -----> Rv + 80*\/3 = 192*(\/3/2) ----> Rv = 16*\/3 N

Já resolví. Você tem o gabarito?

Concordo com 192 e 96

por Leonardo Rêgo Quirino Qua 06 Jun 2012, 19:38

Elcioschin escreveu:Atuam as seguintes forças

1) No apoio A: Força horizontal Rh para a direita e força vertical Rv para cima

2) No ponto B: Reaã normal N perpendicular à barra, (inclinada para cima)

3) Peso P indicado

Projete a força N em eixo horizontal (Nh) e vertical (Nv)

Monte as equações de equlíbrio:

a)Momento em relação ao apoio A
b) Equlíbrio nos DOIS eixos.

Pronto

Já resolví. Você tem o gabarito?

Rh = Nh

Sim mestre!
a) 192N
b)Xa=96N e Ya=16V3N

por Leonardo Rêgo Quirino Qua 06 Jun 2012, 20:29

Eu não sei se minha compreensão na parte das forças estão corretas, no meu entendimento deveriam ficar assim:

Equilíbrio dos corpos extensos Scaled.php?server=138&filename=cecen

Equilíbrio dos corpos extensos Scaled.php?server=138&filename=cecen

Está certo?
Minhas somas dos momentos e somas algébricas das forças estão muito mau organizadas, estou me enrolando todo aqui :scratch:

por **Elcioschin** Qua 06 Jun 2012, 21:24

Leonardo

Seu desenho tem erros:

1) A força N não é vertical: ela é perpedicular ao plano inclinado (um pouco tombada para a esquerda).

2) Ao invés de Nx escreva Nh; além dissoela NÃO fica embaixo e sim atua no ponto B. Complemente com a componente Nv

3) Faltou projetar P no eixo X (que é a própria barra) e no eixo Y (perpendicular a ela)

4) Faça uma correção: coloque Rv para baixo e substitua Rx por Rh

Completei minha solução editando a mensagem anterior

por Leonardo Rêgo Quirino Qua 06 Jun 2012, 22:44

Obrigado Elcioschin, me ajudou bastante para a resolução de questões similares, além de ter esclarecido essa questão claramente!

por passosfil Dom 18 Dez 2016, 20:51

Elcioschin escreveu:Atuam as seguintes forças

1) No apoio A: Força horizontal Rh para a direita e força vertical Rv (para baixo)

2) No ponto B: Reação normal N perpendicular à barra, (inclinada, para cima à esquerda)

3) Peso P indicado

Projete a força N em eixo horizontal (Nh, para a esquerda) e num vertical (Nv, para cima)
Projete a força P (Py) num eixo perpendicular à barra (inclinado para a direita) e no eixo da barra (Px, sentido para o ponto A).

Nh = N*cos60º ---- Nv = N*cos30º -----> Px = P*cos60º = (80*\/3)*(1/2) Px = 40*\/3 -----> Py = P*cos30º = (80*\/3)*(\/3/2) = 120

Monte as equações de equlíbrio:

a)Momento em relação ao apoio A: N*(8 - 3) = Py*8 ----> N*5 = 120*8 ----> N = 192 N

b) Equlíbrio nos eixos vertical e horizontal

Rh = Nh ----> Rh = N*cos60º ----> Rh = 192*(1/2) ----> Rh = 96 N

Rv + P = Nv -----> Rv + 80*\/3 = 192*(\/3/2) ----> Rv = 16*\/3 N

Já resolví. Você tem o gabarito?

Concordo com 192 e 96

Faltou converter de cm para m, mas felizmente deu a resposta correta.

por **Elcioschin** Dom 18 Dez 2016, 21:13

passosfil

Nesta questão não há necessidade de converter de cm para m

Isto acontece porque, como as medidas de distância (80 e 60) estão em cm, estas unidades vão se cancelar nos dois membros. Com isto as forças serão dadas em N

Assim, tanto faz usar 0,8 m e 0,3 m ou 8 dm e 3 dm ou 80 cm e 30 cm

Conclusão o resultado não deu certo "felizmente": deu certo porque a solução foi correta.

por passosfil Seg 19 Dez 2016, 12:37

Elcioschin escreveu:passosfil

Nesta questão não há necessidade de converter de cm para m

Isto acontece porque, como as medidas de distância (80 e 60) estão em cm, estas unidades vão se cancelar nos dois membros. Com isto as forças serão dadas em N

Assim, tanto faz usar 0,8 m e 0,3 m ou 8 dm e 3 dm ou 80 cm e 30 cm

Conclusão o resultado não deu certo "felizmente": deu certo porque a solução foi correta.

Fisicamente não seria correto, pois cm não é igual a m, então permaneço com minha afirmação. As forças estão em N=kg*m/s². Está certo? tá, mas rigorosamente deveria converter. É só chatice mesmo , pois devemos fazer tudo corretamente, mas nada disso invalida sua resposta.

por **Elcioschin** Seg 19 Dez 2016, 12:58

passosfil

Acho que você não entendeu minha explicação; vou detalhar mais:

Veja a equação dos momentos: N.d = Py.D

Py = 120 N
d = AB = AC - BC = 80 - 30 = 50 cm = 5 dm = 0,5 m
D = AC = 80 cm = 8 dm = 0,8 m

Usando a fórmula com cm ---> N.50 cm = (120 N).80 cm ---> cm do 1ª membro cancela com cm do 2º membro ---> N.50 = 120.80 N ---> N = 192 N

Usando a fórmula com dm ---> N.5 dm = (120 N).8 dm ---> dm do 1ª membro cancela com dm do 2º membro ---> N.5 = 120.8 N ---> N = 192 N

Usando a fórmula com m ---> N.0,5 m = (120 N).0,8 m ---> m do 1ª membro cancela com m do 2º membro ---> N.0,5 = 120.0,8 N ---> N = 192 N

Entendeu agora? As unidades estão nos dois membros da equação: elas vão se cancelar, desde que sejam do mesmo tipo. Assim, a resposta do valor da normal N vai sair em newtons (N)

Isto somente pode ser feito (usar cm misturado com N) se houver cancelamento das unidades nos 2 membros.
Nos demais casos deve-se usar m, obrigatoriamente