ITA-Método de Gauss-Jordan (Álgebra Matricial)

por **JOAO [ITA]** Sex 27 Abr 2012, 00:04

Sendo $A=\begin{bmatrix} 1 &2 &-1 \\ 0 &-3 &2 \\ 3 &-1 &-2 \end{bmatrix}$ , então o elemento da terceira linha e primeira coluna, de sua inversa, será igual a:

a) $\frac{5}{8}$

b) $\frac{9}{11}$

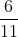
c) $\frac{6}{11}$

d) $-\frac{2}{13}$

e) $\frac{1}{13}$

OBS: A lista não veio com gabarito.

por **hygorvv** Sex 27 Abr 2012, 00:12

Fiz a multiplicação somente para encontrar a primeira coluna, montei um sistema e encontrei 9/11.

Veja, supondo a matriz inversa
A-¹=
[a b c]
[d e f]
[g h i]

Fazendo a multiplicação, temos um sistema formado pela primeira coluna (igualando a matriz identidade)
a+2d-g=1 (i)
-3d+2g=0 (ii)
3a-d-2g=0 (iii)

de (ii), tiramos que d=2g/3
substituindo em (i) e (iii) e fazendo outro sistema, chegamos:
a+g/3=1 (iv)
3a-8g/3=0 (v)
multiplica a primeira por 3 e subtrai com a segunda, obtemos:
g+8g/3=3
g=9/11 que é o que procuramos.

Espero que seja isso e que te ajude.

por **Al.Henrique** Sex 27 Abr 2012, 00:22

Amigo , Faça de modo mais simples e Rápido:

Lembre-se do teorema :

aˉ¹(ij) = Det(A)ˉ¹ . Aji

Denota-se aˉ¹ij como elemento da matriz inversa , Det(A)ˉ¹ é 1/Det(A),ou seja, o inverso do determinante de A e Aji o COFATOR da linha j coluna i.

Queremos portanto aˉ¹(31) = Det(A) . A(13)

Por inspeção,Temos que Det(A) = 11

A(13) é um numero dado, eleminando a primeira linha e a terceria coluna da matriz A, por :

| 0 -3 |
| 3 -1 |

Logo , A(13) = 9

Portanto :

aˉ¹(31) = (1/11) . 9

Que da o gabarito :

aˉ¹(31) = 9/11