Álgebra Matricial - ITA

por **JOAO [ITA]** Qui 26 Abr 2012, 23:18

Sejam $A$ , $B$ e
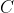$C$ matrizes reais de ordem $n$ e
$O_{n}$ a matriz nula também de ordem $n$ . Considere as afirmações :

I. $AB =BA$

II. $AB =AC \Rightarrow B=C$

III. $A^2 = O_{n}\Rightarrow A = O_{n}$

IV. $(AB)C=A(BC)$

V. $(A-B)^2=A^2-2AB+B^2$

Então podemos afirmar que:

a) Apenas a I é falsa.

b) Apenas a IV é verdadeira.

c) V é verdadeira.

d) II e III são verdadeiras.

e) III e IV são verdadeiras.

OBS: A lista não veio com gabarito.

por **Al.Henrique** Qui 26 Abr 2012, 23:30

I) FALSO
AB ≠ BA
AB = BA se, e somente se, A e B comutem.

II) FALSO

III) VERDADEIRO
Vale para as matrizes, a propriedade associativa.

IV) VERDADEIRO
Se A² = O .'. A.A = O
Supondo que A possua inversa (A*), Multipliquemos por A* dos dois lados da equação:

A.(A.A*) = O.A*
Que podemos dizer :
A.I = O

Como a matriz identidade I é um elementro neutro na multiplicação das matrizes, segue que :

A = O

V) FALSO
Só ocorre se AB = BA

Gabarito : Letra (E)

Álgebra Matricial - ITA

Álgebra Matricial - ITA

Re: Álgebra Matricial - ITA

Um fórum livre e democrático.