IME - Círculo

por **luiseduardo** Ter 27 Mar 2012, 11:26

Relembrando a primeira mensagem :

Em um círculo de 10V2 de diâmetro temos duas cordas medindo 2 e 10. Achar a corda do arco soma dos arcos das cordas anteriores.

gab:

Spoiler:

por **Claudir** Sáb 09 Jul 2016, 18:38

Uma terceira resolução alternativa:

Aproveitando a figura do mestre Raimundo, seja x o valor da corda em questão, que completa o triângulo BCD (x = CD).

Temos a área do triângulo em função do raio do seu circulo circunscrito:

$S=\frac{2.10.x}{4.5\sqrt{2}}\to S^2=\frac{x^2}{2}\ \ \ (I)$

Além disso, também temos a área do triângulo, por Herón:

$\\\\p=6+\frac{x}{2}\\\\S^2=p(p-2)(p-10)(p-x)\\\\S^2=\frac{1}{16}(144-x^2)(x^2-64)\ \ \ (II)$

Igualando as expressões (I) e (II) encontraremos a seguinte equação biquadrada:

$x^4-200x^2+9216=0$

Cujas raízes positivas são 8√2 e 12.

Descartamos a raíz 12 através da desigualdade triangular, pois:

x < 10 + 2

por Nassif Qui 02 Jul 2020, 18:07

Só pra mim que a resolução do Raimundo não está aparecendo?

por **Rory Gilmore** Qui 02 Jul 2020, 18:52

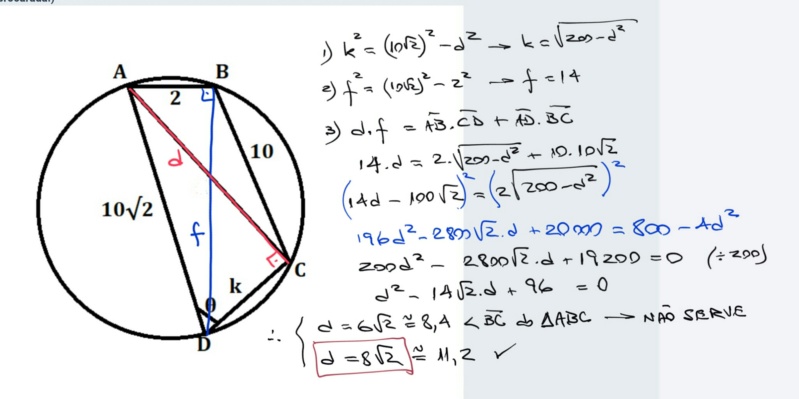
Acompanhe minha solução na imagem abaixo, onde AB = corda de medida 2, BC = corda de medida 10, AD = diâmetro 10√2 e CD = k. ABCD é um quadrilátero inscritível e por isso os ângulos opostos são suplementares.
I) No triângulo retângulo ACD:
cos θ = k/10√2

II) No triângulo retângulo ACD:
(10√2)² = d² + k²
200 = d² + k²
k² = 200 - d²
k = √(200 - d²)

III) Lei dos cossenos no triângulo ABC:
d² = (2)² + (10)² - 2.(2).(10).cos (180 - θ)
d² = 4 + 100 - 40.(- cos θ)
d² = 104 + 40.cos θ
d² = 104 + 40.k/10√2
d² = 104 + 4k/√2
d² = 104 + 4.√(200 - d²)/√2
d = 8√2 (medida da corda procurada.)