FGV/2011
4 participantes
Página 2 de 2
Página 2 de 2 • 
1, 2
FGV/2011
por velloso Qua 22 Fev 2012, 04:37
Relembrando a primeira mensagem :
dado um triangulo de vértices (0,12), (0,0), (5,0) no plano cartesiano ortogonal, a distância entre os centros das circunferências inscrita e circunscrita a esse triângulo é:
a)(3√5)2
b)7/2
c)√15
d)(√65)/2
e)9/2
ps: comando revisado!
dado um triangulo de vértices (0,12), (0,0), (5,0) no plano cartesiano ortogonal, a distância entre os centros das circunferências inscrita e circunscrita a esse triângulo é:
a)(3√5)2
b)7/2
c)√15
d)(√65)/2
e)9/2
ps: comando revisado!
velloso- Estrela Dourada
- Mensagens : 1142
Data de inscrição : 07/04/2010
Idade : 34
Localização : Belém - Pará
velloso- Estrela Dourada
- Mensagens : 1142
Data de inscrição : 07/04/2010
Idade : 34
Localização : Belém - Pará
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Re: FGV/2011
por MarlonBrSKOITO Ter 25 Ago 2020, 19:57
Alguém pode me explicar essa ?
Não entendi nada
Não entendi nada
MarlonBrSKOITO- Jedi
- Mensagens : 235
Data de inscrição : 01/06/2019
Idade : 22
Localização : Barbacena MG
Re: FGV/2011
por Elcioschin Ter 25 Ago 2020, 20:30
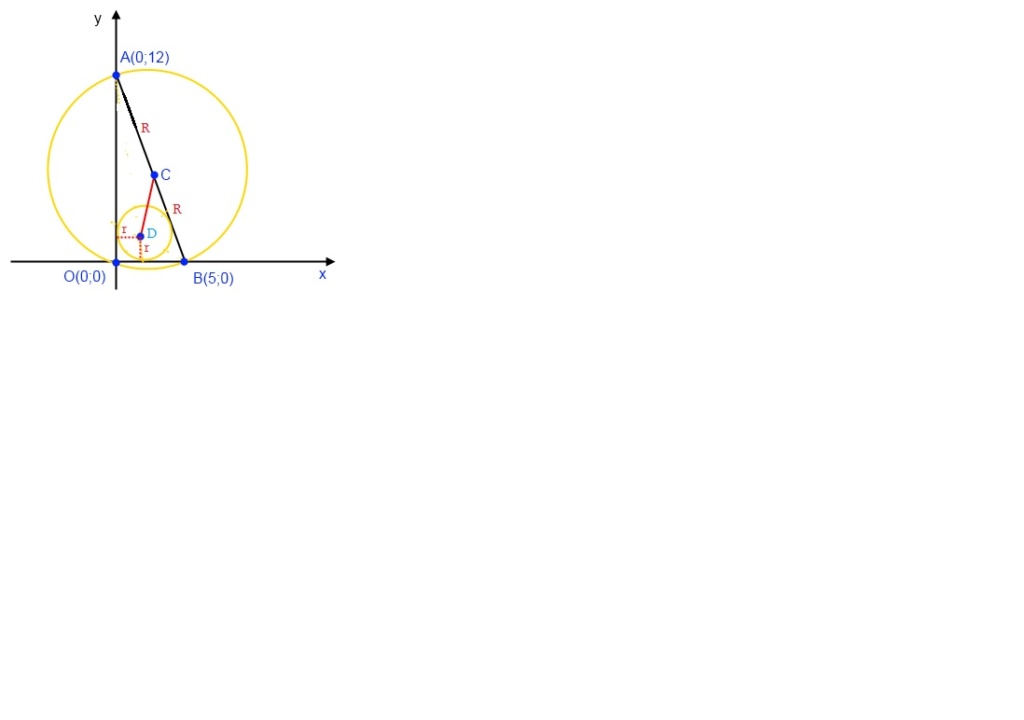
Existe uma solução bem mais simples.
Vou aproveitar a figura postada com ligeiras modificações.
Notem que OAB é um triângulo retângulo com catetos 5 e 12 --> hipotenusa AB = 13
O centro do triângulo circunscrito é o ponto médio M da hipotenusa: M(5/2, 6)
O raio r da circunferência inscrita em qualquer triângulo retângulo é dado por:
r = (b + c - a)/2 ---> r = (5 + 12 - 13)/2 ---> r = 2
O incentro é D(2, 2)
DM² = (5/2 - 2)² + (6 - 20² ---> DM = √65/2
Vou aproveitar a figura postada com ligeiras modificações.
Notem que OAB é um triângulo retângulo com catetos 5 e 12 --> hipotenusa AB = 13
O centro do triângulo circunscrito é o ponto médio M da hipotenusa: M(5/2, 6)
O raio r da circunferência inscrita em qualquer triângulo retângulo é dado por:
r = (b + c - a)/2 ---> r = (5 + 12 - 13)/2 ---> r = 2
O incentro é D(2, 2)
DM² = (5/2 - 2)² + (6 - 20² ---> DM = √65/2
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 2 de 2 • 1, 2
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
