Soluções da equação

por gabriel93 Dom 25 Dez 2011, 21:42

Encontre todas as soluções inteiras de:

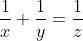
$\frac{1}{x} + \frac{1}{y} = \frac{1}{z}$

por **ivomilton** Dom 25 Dez 2011, 22:44

gabriel93 escreveu:Encontre todas as soluções inteiras de:

$\frac{1}{x} + \frac{1}{y} = \frac{1}{z}$

Boa noite, Gabriel.

1/x + 1/y = 1/z → mmc(x,y,z) = xyz → colocando, então, tudo sobre denominador xyz, fica:

yz/xyz + xz/xyz = xy/xyz → multiplicando tudo pelo denominador xyz, o eliminaremos:

yz + xz = xy
z(x+y) = xy
z = xy/(x+y)

A última equação nos mostra que o numerador "xy" deverá ser divisível por "x+y" para que se obternha "z" inteiro.

Fazendo algumas tentativas numéricas, encontrei que fazendo:
x = 3
y = 6
x+y = 9

obteremos:
z = xy/(x+y) = 3*6/9 = 18/9 = 2

Donde uma das soluções seria:
1/3 + 1/6 = 1/2 (*)

Observei, mais, que o segundo número (6) é igual ao produto do primeiro (3) por 2 (onde 2 = 3-1).
A partir dessa segunda observação, e experimentando fazer x=4, obtive:
x = 4
y = 4*(4-1) = 4*3 = 12
x+y = 4+12 = 16

obtendo-se:
z = xy/(x+y) = 4*12/16 = 48/16 = 3

Donde esta outra solução seria:
1/4 + 1/12 = 1/3 (**)

Colocando a experiência realizada em forma algébrica, ficaria:
x = x
y = x*(x-1)

xy = x*[x*(x-1)] = x²(x-1) = x³ - x²
x+y = x + x*(x-1) = x + x² - x = x²

z = xy/(x+y) = (x³ - x²)/x² = x - 1

Concluindo, teríamos que:
x = x
y = x² - x
z = x - 1

donde:

.. 1 ........ 1 ........ 1
------ + ------ = -------
.. x ...... x²-x .... x - 1

Contudo, atentando melhor para a formação dos denominadores de (*) e (**), percebi que:
6 = 3*2
12 = 4*3

Donde podemos definir assim:
1/x + 1/xz = 1/z

Poderemos assim variar à vontade os valores de "x" e "z" dentro do universo de N* (naturais exceto o zero), fazendo sempre "z" menor que "x" .
Temos, portanto, infinitas soluções para essa questão — sempre considerando que os denominadores seriam positivos.

Um feliz Natal e um abençoado Ano Novo para você!