Prisma triangular oblíquo

A base de um prisma oblíquo é um triângulo equilátero de lado a. A aresta lateral forma 60º com o plano da base. Um dos vértices da base superior tem projeção ortogonal sobre o plano da base no centro da circunferência. Calcule a altura do prisma e a área de cada face lateral.

\( Gabarito:a; \frac{2a^2 \sqrt3}{3}; \frac{a^2 \sqrt39}{6}; \frac{a^2 \sqrt39}{6}\)
As respostas referem-se à altura do prisma e à área de cada face, respectivamente.

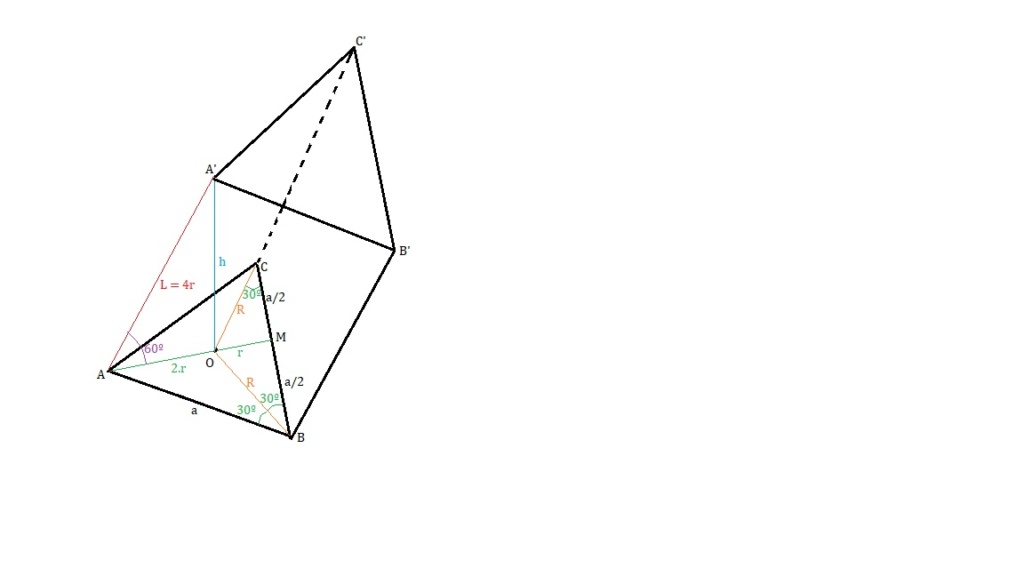
Seja ABC a base inferior e A'B'C' a base superior 
Seja M o ponto médio de BC = a ---> BM = CM = a/2
Seja O o centro das circunferências inscrita (raio r) e circunscrita (raio R) na base 

Seja A' o vértice que fica exatamente acime de O --->A'O = h

2.R.cos30º = a ---> 2.R.(√3/2) = a --> R = a.√3/3 ---> R² = a²/3

r² = R² - (a/2)² ---> r² = a²/3 - a²/4 ---> r² = a²/12 ----> r = a.√3/6

OM = r ---> OA = 2.r ---> A'ÂO = 60º

A'A = L ---> A'A.cos60º = OA ---> L.(1/2) = 2.r ---> L = 4.r 

h = L.sen60º --->  h = (4.r).(√3/2) ---> h = r.2√3 ---> h = ( a.√3/6).(√3/2) ---> h = a

Complete

Olá, Elcio! Entendi perfeitamente suas explicações!
Mas como eu poderia encontrar essas áreas? Achei que um "base x altura" do paralelogramo já bastaria, mas, além de não funcionar, achei estranho uma só área ter valor diferente das demais.