Segunda Fase Unesp, Geometria Plana

por lukazzz Sex 17 Fev 2023, 19:08

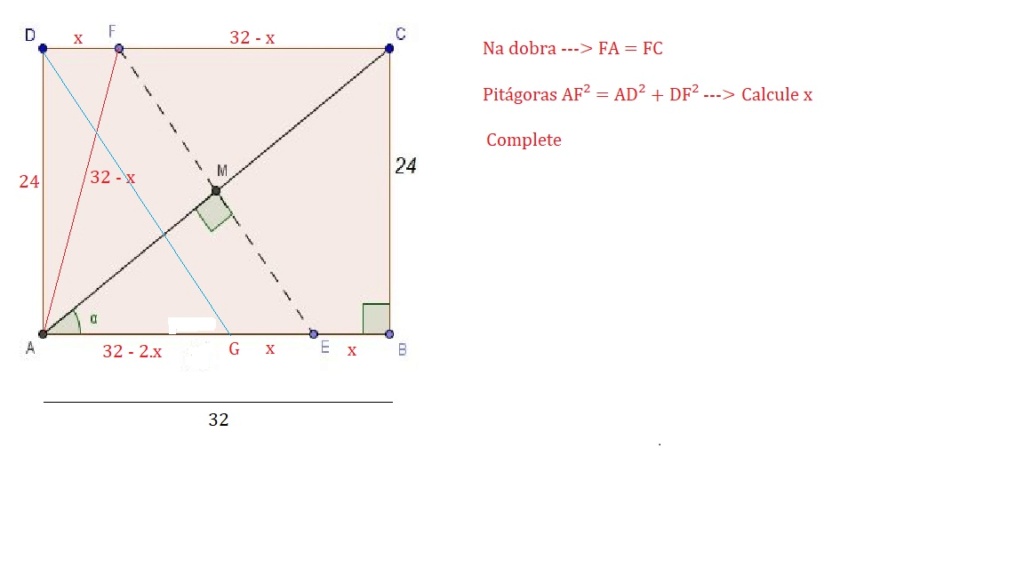
(UNESP).Uma folha de papel retangular de 24 cm por 32 cm é dobrada de maneira que os vértices opostos se toquem.
Ache o comprimento da dobra.

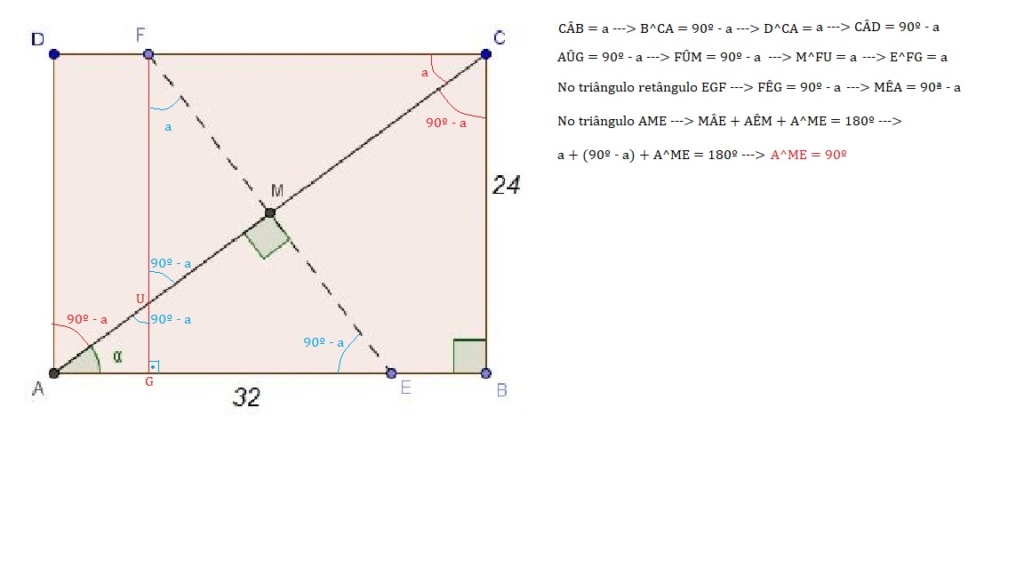
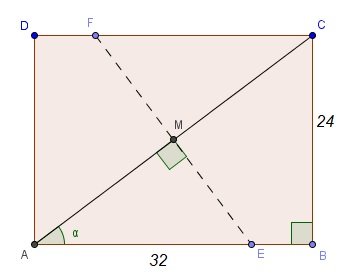
Não consegui resolver essa questão, a única resolução que achei não entendi o porquê do angulo de 90º entre os segmentos de reta AM e ME, que esta na imagem, a semelhança de triangulo após isso fica fácil, mas não consigo entender de onde saiu esse ângulo, visto que o exercício não possui imagem... ficarei extremamente grato se puderem me ajudar...

Segunda Fase Unesp, Geometria Plana File

Segunda Fase Unesp, Geometria Plana File

Gabarito: 30 cm

por **Elcioschin** Sex 17 Fev 2023, 19:20

Poste a resolução que vc tem, com a imagem.

por **Elcioschin** Sex 17 Fev 2023, 19:34

Você não postou a solução.

Segunda Fase Unesp, Geometria Plana Dobra11

por lukazzz Sex 17 Fev 2023, 19:46

Por Pitágoras,

AC²=3²+24² →AC=40

Se M não fosse ponto médio de AC, ao dobrarmos a folha, A não encontraria C. Logo, M é ponto médio de AC, e, portanto,

AM = AC/2 =20.

Agora, repare que ABC e AEM são semelhantes por AA e, portanto:

AE/AM = AC/AB → AE = 20 x 40/32=25

E, prosseguindo,

EM/BC = AE/AC → EM = 24 x 25/40 = 15

Se M não fosse ponto médio de EF, ao dobrarmos a folha, A não encontraria C. Logo, M é ponto médio de EF, e, portanto,

EF = 2xEM = 2x15 =30

[ltr] Segunda Fase Unesp, Geometria Plana File

[/ltr]

por lukazzz Sex 17 Fev 2023, 19:50

A resolução, a partir da dedução que o ângulo compreendido entre os segmentos AM e ME é de 90º, faz todo sentido. Porém, eu n consigo achar qual foi o raciocínio pra se chegar a essa informação... Lembrando que essa imagem não faz parte do exercício, foi posta para exemplificar o raciocínio da resoluçao. Pelo seu desenho fez muito mais sentido, entendi perfeitamente, muito obrigado. Mas se puder me ajudar a entender de onde saiu o angulo de 90 da primeira resoluçao ficarei mt grato...

por **Elcioschin** Sáb 18 Fev 2023, 10:37

por lukazzz Seg 20 Fev 2023, 12:45

muitíssimo obrigado!!!!

por Carlos Heitor (EPCAr) Seg 20 Fev 2023, 14:56

lukazzz escreveu:(UNESP).Uma folha de papel retangular de 24 cm por 32 cm é dobrada de maneira que os vértices opostos se toquem.
Ache o comprimento da dobra.

Não consegui resolver essa questão, a única resolução que achei não entendi o porquê do angulo de 90º entre os segmentos de reta AM e ME, que esta na imagem, a semelhança de triangulo após isso fica fácil, mas não consigo entender de onde saiu esse ângulo, visto que o exercício não possui imagem... ficarei extremamente grato se puderem me ajudar...

Gabarito: 30 cm

Boa tarde, parceiro. Tu poderias provar que esse ângulo era reto, como o mestre Elcioschin fez, mas isso poderia ser concluído mais facilmente por simetria, por isso o autor da resolução anterior não provou. Repare que ao dobrar uma folha até sua ponta, a dobra é transversal a diagonal vindo da dessa ponta, se não for, é porque ele está na direção da ponta. Faça o teste com um papel e reflita sobre isso que você notará que dá para se concluir isso.