Retas em R3
2 participantes
Página 1 de 1
 Retas em R3
Retas em R3
Considere dois numeros α, β ∈ R e as retas em R3
r1 : (x-1)/ −2 = y − 2 = (z − 3)/ −1 e r2 : X = (1, α, 3) + λ(β, 3, −3).
(a) Determine todos os α, β ∈ R tais que: r1 e r2 sejam paralelas e distintas.
(b) Determine todos os α, β ∈ R tais que: r1 e r2 sejam reversas.
(c) Determine todos os α, β ∈ R tais que: r1 e r2 sejam concorrentes (r1 ∩ r2 e um ponto).
r1 : (x-1)/ −2 = y − 2 = (z − 3)/ −1 e r2 : X = (1, α, 3) + λ(β, 3, −3).
(a) Determine todos os α, β ∈ R tais que: r1 e r2 sejam paralelas e distintas.
(b) Determine todos os α, β ∈ R tais que: r1 e r2 sejam reversas.
(c) Determine todos os α, β ∈ R tais que: r1 e r2 sejam concorrentes (r1 ∩ r2 e um ponto).
Julious3451- Iniciante
- Mensagens : 1
Data de inscrição : 15/12/2021
 Re: Retas em R3
Re: Retas em R3
Olá.
Precisamos de apenas um ponto e um vetor para caracterizar uma reta concorda? O vetor é livre, passa a ser fixo quando escolhemos um ponto, e esse vetor fornece a direção da reta. Portanto, uma reta em 3 dimensões tem a seguinte cara:
[latex]P=P_0+\vec{v}t[/latex]
[latex]P=P_0+(x,y,z)t[/latex]
U vetor é caracterizado por três coordenadas, ou, como a soma de 3 vetores da base canônica, podemos escrever essa reta da seguinte forma:
[latex](x,y,z)=(x_0,y_0,z_0)+(x,y,z)t[/latex]
Isto é:
[latex]\left\{\begin{matrix} x=x_0+ u_1t& & \\ y=y_0+u_2t& & \\ z=z_0+u_3t& & \end{matrix}\right.[/latex]
Se eliminarmos t do sistema obtemos:
[latex]\frac{x-x_0}{u_1}=\frac{y-y_0}{u_2}=\frac{z-z_0}{u_3}[/latex]
Poranto, por comparação, obtemos a seguinte equação de reta:
[latex]R=(1,2,3)+(-2,1,3)t[/latex]
Resta agora responder as perguntas
a) Quando duas retas são paralelas? Quando o vetor que as definem são paralelos, óbvio, então, precisamos que o vetor da reta R2 e o vetor que encontramos sejam múltiplo um do outro, para serem distintas, devem passam por pontos diferentes, então o ponto de uma tem que ser diferente do ponto de outra, tente terminar.
b) Essa condição, geometricamente é muito simples, mas se não visualizar geometricamente pode parece uma fórmula sem sentido. Primeira coisa. O determinante de 3 vetores calcula o volume do paralelepípedo gerado por eles (Leve isso por todo curso de geometria analítica, é importante, sério). Pense comigo, quando que o determinante de 3 vetores é zero? Quando o volume do paralelepípedo é zero, não é mesmo? Então, precisamos formar um paralelepípedo de volume diferente de zero para garantir que não sejam coplanares, veja a figura:

As duas retas são exemplos de retas reversas, vamos construir o vetor que parte de um ponto de uma e chega em um ponto de outra:
[latex]\vec{u}=(1-1,a-2,3-3)=(0,a-2,0)[/latex]
Basta tomar um ponto menos o outro, por fim, precisamos que o volume do paralelepípedo
[latex]V=\begin{vmatrix} 0 &a-2 &0 \\ \beta &3 &-3 \\ -2 &1 &3 \end{vmatrix} \neq 0[/latex]
Basta resolver a equação, lembrando que nesse caso, beta deve ser tal que o vetor de uma reta não seja paralelo ao vetor da outra. Isso garante a reversidade.

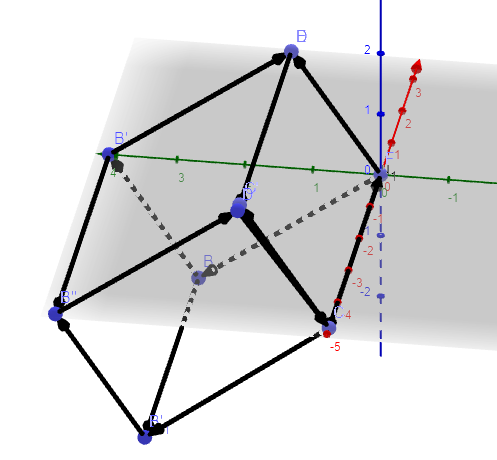
Na figura, desenhei o paralelepípedo de um dos casos de reta reversa, veja que de fato é diferente de zero o determinante, pois o volume é zero, se o volume fosse zero, concluiríamos que os 3 vetores são LD, logo não podem ser reversas.
c) Pelo mesmo argumento, agora, fazer o determinante acima ser igual a zero garante que as retas estão no mesmo plano. Mas ainda podem ser PARALELAS! Então, precisamos garantir que um vetor não seja paralelo ao outro .
.
Tente encontrar os valores, qualquer coisa me fala, abraços.
Precisamos de apenas um ponto e um vetor para caracterizar uma reta concorda? O vetor é livre, passa a ser fixo quando escolhemos um ponto, e esse vetor fornece a direção da reta. Portanto, uma reta em 3 dimensões tem a seguinte cara:
[latex]P=P_0+\vec{v}t[/latex]
[latex]P=P_0+(x,y,z)t[/latex]
U vetor é caracterizado por três coordenadas, ou, como a soma de 3 vetores da base canônica, podemos escrever essa reta da seguinte forma:
[latex](x,y,z)=(x_0,y_0,z_0)+(x,y,z)t[/latex]
Isto é:
[latex]\left\{\begin{matrix} x=x_0+ u_1t& & \\ y=y_0+u_2t& & \\ z=z_0+u_3t& & \end{matrix}\right.[/latex]
Se eliminarmos t do sistema obtemos:
[latex]\frac{x-x_0}{u_1}=\frac{y-y_0}{u_2}=\frac{z-z_0}{u_3}[/latex]
Poranto, por comparação, obtemos a seguinte equação de reta:
[latex]R=(1,2,3)+(-2,1,3)t[/latex]
Resta agora responder as perguntas
a) Quando duas retas são paralelas? Quando o vetor que as definem são paralelos, óbvio, então, precisamos que o vetor da reta R2 e o vetor que encontramos sejam múltiplo um do outro, para serem distintas, devem passam por pontos diferentes, então o ponto de uma tem que ser diferente do ponto de outra, tente terminar.
b) Essa condição, geometricamente é muito simples, mas se não visualizar geometricamente pode parece uma fórmula sem sentido. Primeira coisa. O determinante de 3 vetores calcula o volume do paralelepípedo gerado por eles (Leve isso por todo curso de geometria analítica, é importante, sério). Pense comigo, quando que o determinante de 3 vetores é zero? Quando o volume do paralelepípedo é zero, não é mesmo? Então, precisamos formar um paralelepípedo de volume diferente de zero para garantir que não sejam coplanares, veja a figura:

As duas retas são exemplos de retas reversas, vamos construir o vetor que parte de um ponto de uma e chega em um ponto de outra:
[latex]\vec{u}=(1-1,a-2,3-3)=(0,a-2,0)[/latex]
Basta tomar um ponto menos o outro, por fim, precisamos que o volume do paralelepípedo
[latex]V=\begin{vmatrix} 0 &a-2 &0 \\ \beta &3 &-3 \\ -2 &1 &3 \end{vmatrix} \neq 0[/latex]
Basta resolver a equação, lembrando que nesse caso, beta deve ser tal que o vetor de uma reta não seja paralelo ao vetor da outra. Isso garante a reversidade.


Na figura, desenhei o paralelepípedo de um dos casos de reta reversa, veja que de fato é diferente de zero o determinante, pois o volume é zero, se o volume fosse zero, concluiríamos que os 3 vetores são LD, logo não podem ser reversas.
c) Pelo mesmo argumento, agora, fazer o determinante acima ser igual a zero garante que as retas estão no mesmo plano. Mas ainda podem ser PARALELAS! Então, precisamos garantir que um vetor não seja paralelo ao outro
Tente encontrar os valores, qualquer coisa me fala, abraços.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












