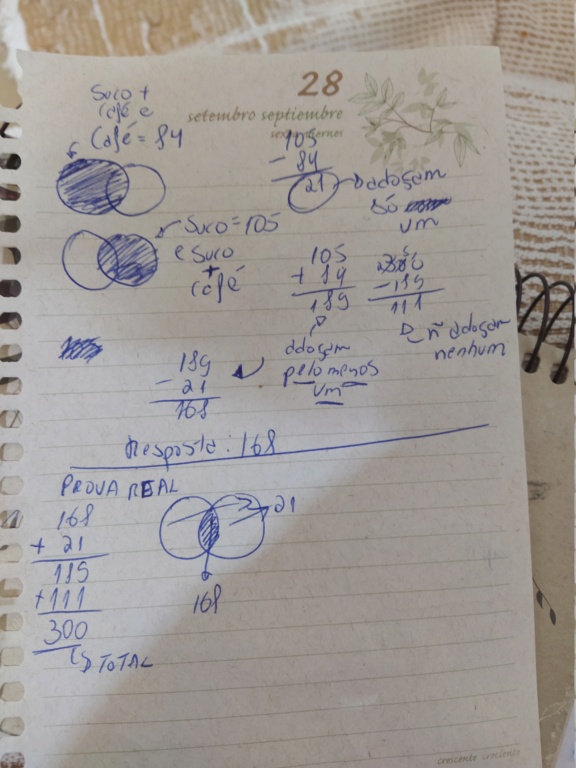Diagrama de Venn
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Diagrama de Venn
Diagrama de Venn
Uma pesquisa foi feita para tentar descobrir um pouco mais sobre o gosto das pessoas na hora de adoçar o café e o suco. 28% dos indivíduos dizem gostar de adoçar o café. 35% dizem gostar de adoçar o suco. Se a pesquisa foi realizada com 300 pessoas, então a quantidade delas que gosta de adoçar o café e gosta de adoçar o suco é:
A) Entre 0 e 80.
B) Entre 80 e 120.
C) Entre 120 e 170.
D) Entre 170 e 200.
E) Superior a 200.
Ps: não tenho o gabarito
A) Entre 0 e 80.
B) Entre 80 e 120.
C) Entre 120 e 170.
D) Entre 170 e 200.
E) Superior a 200.
Ps: não tenho o gabarito

Ceruko- Estrela Dourada

- Mensagens : 1326
Data de inscrição : 01/07/2020
Idade : 23
Localização : Ribeirão Preto

jopagliarin- Jedi

- Mensagens : 399
Data de inscrição : 13/10/2019
Idade : 22
Localização : Curitiba/PR \\ Joaçaba/SC
 Re: Diagrama de Venn
Re: Diagrama de Venn
Então a resposta seria 21 pessoas?

Ceruko- Estrela Dourada

- Mensagens : 1326
Data de inscrição : 01/07/2020
Idade : 23
Localização : Ribeirão Preto
 Re: Diagrama de Venn
Re: Diagrama de Venn
A questão pede a intersecção, quem gosta de adoçar o café e suco.
Nós temos o conjunto C que é quem gosta de adoçar o café e café+suco e temos o conjunto S que é quem gosta de adoçar o suco e café+suco. Então temos elementos de C que estão em S e o contrário também é verdadeiro. Temos que eliminar esses elementos comuns aos dois conjuntos. Quando eliminamos, restam as pessoas que gostam de adoçar só o café e que gostam de adoçar só o suco e essas são as 21 pessoas (ou um ou outro, e não um e outro). Agora, se somarmos o conjunto C com S, teremos as pessoas que gostam de adoçar pelo menos uma das bebidas. Se eu pegar esse conjunto e eliminar as pessoas que gostam de adoçar apenas uma bebida, teremos as pessoas que gostam de adoçar as duas bebidas e é o que a questão pede. Para mim, a resposta seria 168. Olhe o diagrama q eu esbocei abaixo ("prova real").
Nós temos o conjunto C que é quem gosta de adoçar o café e café+suco e temos o conjunto S que é quem gosta de adoçar o suco e café+suco. Então temos elementos de C que estão em S e o contrário também é verdadeiro. Temos que eliminar esses elementos comuns aos dois conjuntos. Quando eliminamos, restam as pessoas que gostam de adoçar só o café e que gostam de adoçar só o suco e essas são as 21 pessoas (ou um ou outro, e não um e outro). Agora, se somarmos o conjunto C com S, teremos as pessoas que gostam de adoçar pelo menos uma das bebidas. Se eu pegar esse conjunto e eliminar as pessoas que gostam de adoçar apenas uma bebida, teremos as pessoas que gostam de adoçar as duas bebidas e é o que a questão pede. Para mim, a resposta seria 168. Olhe o diagrama q eu esbocei abaixo ("prova real").

jopagliarin- Jedi

- Mensagens : 399
Data de inscrição : 13/10/2019
Idade : 22
Localização : Curitiba/PR \\ Joaçaba/SC
Ceruko gosta desta mensagem
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos