Morgado II - Divisão Harmônica
2 participantes
Página 1 de 1
Morgado II - Divisão Harmônica
por castelo_hsi Seg 25 Out 2021, 20:29
Os lados ABC de um triângulo medem AB = 6 cm, AC = 9 cm e BC = 11 cm. Se J é o ponto de tangência do círculo exinscrito relativo ao lado c com lado AB e se JL é paralelo a BC, então AL vale:
a) 3 cm
b) 6 cm
c) 7/2 cm
d) 9/2 cm
e) N.R.A
a) 3 cm
b) 6 cm
c) 7/2 cm
d) 9/2 cm
e) N.R.A
- gabarito:
- B
- Observação:
- Essa questão está no capítulo de divisão harmônica do volume II do livro de Geometria Plana do Morgado, divisão harmônica pode ser um caminho porém eu não consegui resolver.
Última edição por castelo_hsi em Ter 26 Out 2021, 17:12, editado 2 vez(es)
castelo_hsi- Mestre Jedi
- Mensagens : 625
Data de inscrição : 27/06/2021
Localização : São Paulo - SP
Re: Morgado II - Divisão Harmônica
por castelo_hsi Ter 26 Out 2021, 16:52
Chamando de P o ponto de tangência do prolongamento de AC e de Q o ponto de tangência na circunferência do prolongamento de BC. Além disso, AL = z. Temos:
AJ = AP = x
JB = BQ = y
x + y = 6cm (I)
BC + y = AC + x ---> x - y = 11 - 9 ---> x - y = 2cm (II)
Somando (I) e (II) ---> 2x = 8 .:. x = 4cm e y = 2cm
Aplicando o Teorema de Tales, teremos:
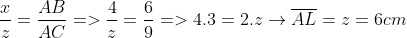
AJ = AP = x
JB = BQ = y
x + y = 6cm (I)
BC + y = AC + x ---> x - y = 11 - 9 ---> x - y = 2cm (II)
Somando (I) e (II) ---> 2x = 8 .:. x = 4cm e y = 2cm
Aplicando o Teorema de Tales, teremos:
castelo_hsi- Mestre Jedi
- Mensagens : 625
Data de inscrição : 27/06/2021
Localização : São Paulo - SP
raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
castelo_hsi gosta desta mensagem
Tópicos semelhantes» (Morgado - Geo. Plana) - Divisão Harmônica
» Divisão harmônica
» Divisão harmônica
» Divisão Harmônica
» Divisão harmônica
» Divisão harmônica
» Divisão harmônica
» Divisão Harmônica
» Divisão harmônica
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
