vetores

Na figura, temos três vetores coplanares formando uma linha
poligonal fechada. A respeito, vale a relação:


Não coloquei as alternativas pois estava dando um erro na hora de passa-las. Eu sei da regra do fórum que as questões tem que vir todas escritas e com suas alternativas...
Duvida : eu entendi que a soma dos vetores gera uma resultante 0, mas porque a ''b'' está errada? Perceba que se eu somar o vetor b ao c a resultante é o vetor a
Gabarito: C

Para somar vetores eles tem que ter o mesmo ponto de aplicação.
Para obter isto precisamos deslizar b, na mesma direção e sentido:

Obrigado pela resposta Mestre !
uma duvida: só posso somar vetores vindo da mesma origem ?
estava pensando no método poligonal em que a extremidade de B junto com a origem do C  iria gerar a resultante A

O que eu disse vale para dois vetores.
No caso de um polígono deve-se examinar caso a caso.

Mestre, obrigado novamente!
porém eu ainda tenho duvidas: nesse caso, por exemplo, ocorre a soma de vetores sem estarem em ponto comum. Como penso nesse exemplo ?
peço desculpas pelo incômodo e agradeço o tempo.

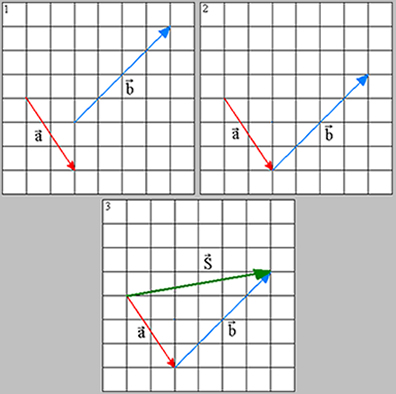
Neste caso dá na mesma:

Na 1ª figura:

Seja A o ponto de aplicação do vetor a (no alto à esquerda)
Seja B o ponto de aplicação do vetor b (embaixo à esquerda)

Desloque B até A de modo que o ponto de aplicação de ambos seja o mesmo.
Pela Regra do paralelogramo trace o vetor S = a + b

Você verá que S tem o mesmo módulo, direção e sentido de S (verde) da 3ª figura.

De fato, tem mesmo.
No entanto, a ultima duvida( me desculpando pela insistência):
No caso da figura com vetores coloridos( azul  vermelho e verde), tanto faz fazer pelo  metodo poligonal ou paralelogramo.
Mas porque não poderia aplicar na imagem inicial?
Assim como os vetores coloridos, os da imagem inicial não tem origem comum e  as extremidades  estão ligadas com origens respeitando o metodo poligonal
Naquele caso o vetor b + vetor c me geraria o vetor a. Que me conduziria a letra b( porque em um caso eu levo em consideração eles terem origens comuns e no outro caso não?).
Novamente agradeço a paciência Elcio, e também peço desculpas pela ignorância

Tanto o método de coincidir os pontos de aplicação de a, b, quanto o método da poligonal de a, b levam ao mesmo resultado da soma S: mesmo módulo, mesma direção (vetores S paralelos) e mesmo sentido (para direita e para cima)

Tentar adivinhar o vetor S sem usar um destes dois métodos, poderá levar a erro.

Sugiro escolher um deles para resolver questões deste tipo, sem errar!

Além dos métodos expostos, vai um apanhado: depois de unir os dois vetores em um mesmo ponto (imagem 2), podemos decompor os vetores em componentes horizontais e verticais. 

Admitindo que o quadriculado trata-se de um quadrado de lado com uma unidade de comprimento (u. c.), temos que: o vetor vermelho tem duas unidades para direita e três unidades para baixo, já o vetor azul tem quatro unidades para a direita e quatro unidades para cima. Aplicando o somatório vetorial nas componentes horizontais e verticais, temos que:



A notação i, j, k, representa cada eixo ordenado, como se fosse (x, y, z). 

Ou seja, temos que o somatório vetorial entre a e b, resulta em um vetor com seis unidades para a direita e uma unidade para cima. Essa maneira e abordagem é muito utilizado na física principalmente.

Representação gráfica dos vetores decompostos: